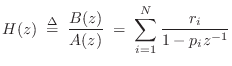Modal Representation
One of the filter structures introduced in Book II [449, p.
209] was the parallel second-order filter bank, which
may be computed from the general transfer function (a ratio of
polynomials in ![]() ) by means of the Partial Fraction Expansion
(PFE) [449, p. 129]:
) by means of the Partial Fraction Expansion
(PFE) [449, p. 129]:
where
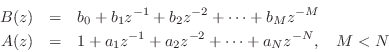
The PFE Eq.![]() (1.12) expands the (strictly proper2.10) transfer function as a
parallel bank of (complex) first-order resonators. When the
polynomial coefficients
(1.12) expands the (strictly proper2.10) transfer function as a
parallel bank of (complex) first-order resonators. When the
polynomial coefficients ![]() and
and ![]() are real, complex poles
are real, complex poles ![]() and
residues
and
residues ![]() occur in conjugate pairs, and these can be
combined to form second-order sections [449, p. 131]:
occur in conjugate pairs, and these can be
combined to form second-order sections [449, p. 131]:
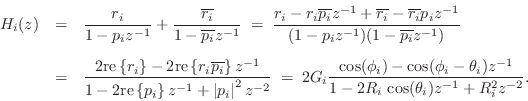
where
![]() and
and
![]() . Thus, every transfer function
. Thus, every transfer function ![]() with real
coefficients can be realized as a parallel bank of real first- and/or
second-order digital filter sections, as well as a parallel FIR branch
when
with real
coefficients can be realized as a parallel bank of real first- and/or
second-order digital filter sections, as well as a parallel FIR branch
when ![]() .
.
As we will develop in §8.5, modal synthesis employs a ``source-filter'' synthesis model consisting of some driving signal into a parallel filter bank in which each filter section implements the transfer function of some resonant mode in the physical system. Normally each section is second-order, but it is sometimes convenient to use larger-order sections; for example, fourth-order sections have been used to model piano partials in order to have beating and two-stage-decay effects built into each partial individually [30,29].
For example, if the physical system were a row of tuning forks (which are designed to have only one significant resonant frequency), each tuning fork would be represented by a single (real) second-order filter section in the sum. In a modal vibrating string model, each second-order filter implements one ``ringing partial overtone'' in response to an excitation such as a finger-pluck or piano-hammer-strike.
State Space to Modal Synthesis
The partial fraction expansion works well to create a modal-synthesis system from a transfer function. However, this approach can yield inefficient realizations when the system has multiple inputs and outputs, because in that case, each element of the transfer-function matrix must be separately expanded by the PFE. (The poles are the same for each element, unless they are canceled by zeros, so it is really only the residue calculations that must be carried out for each element.)
If the second-order filter sections are realized in direct-form-II or transposed-direct-form-I (or more generally in any form for which the poles effectively precede the zeros), then the poles can be shared among all the outputs for each input, since the poles section of the filter from that input to each output sees the same input signal as all others, resulting in the same filter state. Similarly, the recursive portion can be shared across all inputs for each output when the filter sections have poles implemented after the zeros in series; one can imagine ``pushing'' the identical two-pole filters through the summer used to form the output signal. In summary, when the number of inputs exceeds the number of outputs, the poles are more efficiently implemented before the zeros and shared across all outputs for each input, and vice versa. This paragraph can be summarized symbolically by the following matrix equation:
![$\displaystyle \left[\begin{array}{c} y_1 \\ [2pt] y_2 \end{array}\right]
\eqsp...
...{\frac{1}{A}\left[\begin{array}{c} u_1 \\ [2pt] u_2 \end{array}\right]\right\}
$](http://www.dsprelated.com/josimages_new/pasp/img306.png)
What may not be obvious when working with transfer functions alone is
that it is possible to share the poles across all of the inputs
and outputs! The answer? Just diagonalize a state-space
model by means of a similarity transformation [449, p.
360]. This will be discussed a bit further in
§8.5. In a diagonalized state-space model, the ![]() matrix is diagonal.2.11 The
matrix is diagonal.2.11 The ![]() matrix provides
routing and scaling for all the input signals driving the modes. The
matrix provides
routing and scaling for all the input signals driving the modes. The
![]() matrix forms the appropriate linear combination of modes for each
output signal. If the original state-space model is a physical model,
then the transformed system gives a parallel filter bank that is
excited from the inputs and observed at the outputs in a physically
correct way.
matrix forms the appropriate linear combination of modes for each
output signal. If the original state-space model is a physical model,
then the transformed system gives a parallel filter bank that is
excited from the inputs and observed at the outputs in a physically
correct way.
Force-Driven-Mass Diagonalization Example
To diagonalize our force-driven mass example, we may begin with its
state-space model Eq.![]() (1.9):
(1.9):
![$\displaystyle \left[\begin{array}{c} x_{n+1} \\ [2pt] v_{n+1} \end{array}\right...
...t[\begin{array}{c} 0 \\ [2pt] T/m \end{array}\right] f_n, \quad n=0,1,2,\ldots
$](http://www.dsprelated.com/josimages_new/pasp/img307.png)
Typical State-Space Diagonalization Procedure
As discussed in [449, p. 362] and exemplified in
§C.17.6, to diagonalize a system, we must find the
eigenvectors of ![]() by solving
by solving
| (2.13) |
where
The transformed system describes the same system as in Eq.
Efficiency of Diagonalized State-Space Models
Note that a general ![]() th-order state-space model Eq.
th-order state-space model Eq.![]() (1.8) requires
around
(1.8) requires
around ![]() multiply-adds to update for each time step (assuming the
number of inputs and outputs is small compared with the number of
state variables, in which case the
multiply-adds to update for each time step (assuming the
number of inputs and outputs is small compared with the number of
state variables, in which case the
![]() computation dominates).
After diagonalization by a similarity transform, the time update is
only order
computation dominates).
After diagonalization by a similarity transform, the time update is
only order ![]() , just like any other efficient digital filter
realization. Thus, a diagonalized state-space model (modal
representation) is a strong contender for applications in which
it is desirable to have independent control of resonant modes.
, just like any other efficient digital filter
realization. Thus, a diagonalized state-space model (modal
representation) is a strong contender for applications in which
it is desirable to have independent control of resonant modes.
Another advantage of the modal expansion is that frequency-dependent characteristics of hearing can be brought to bear. Low-frequency resonances can easily be modeled more carefully and in more detail than very high-frequency resonances which tend to be heard only ``statistically'' by the ear. For example, rows of high-frequency modes can be collapsed into more efficient digital waveguide loops (§8.5) by retuning them to the nearest harmonic mode series.
Next Section:
Equivalent Circuits
Previous Section:
Transfer Functions