DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Nonlinear Piano-String Equations of Motion in State-Space Form

For the flexible (non-stiff) mass-spring string, referring to Fig.9.26 and Eq.$ \,$(9.34), we have the following equations of motion:

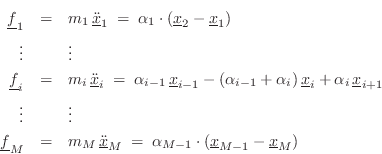
\begin{eqnarray*} \underline{f}_1 &=& m_1 \,\underline{{\ddot x}}_1 \eqsp \alpha... ...M \eqsp \alpha_{M-1}\cdot(\underline{x}_{M-1} - \underline{x}_M) \end{eqnarray*}

or, in $ 3M\times1$ vector form,

$\displaystyle \underline{F}\eqsp \mathbf{M}\, \ddot{\underline{X}} \eqsp \mathbf{A}\, \underline{X}. $

Here the string terminations (bridge and agraffe) are modeled simply as very large masses $ m_1$ and $ m_M$.

Next Section:
Finite Difference Implementation
Previous Section:
A Stiff Mass-Spring String Model