Numerical Integration of General State-Space Models
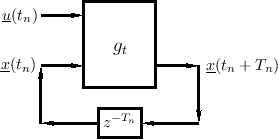
An approximate discrete-time numerical solution of Eq.
(1.6) is provided by
![$\displaystyle \underline{x}(t_n+T_n) \eqsp \underline{x}(t_n) + T_n\,f[\underline{x}(t_n),\underline{u}(t_n)], \quad n=0,1,2,\ldots\,. \protect$](http://www.dsprelated.com/josimages_new/pasp/img217.png){kind=small}
Let
![$\displaystyle g_{t_n}[\underline{x}(t_n),\underline{u}(t_n)] \isdefs \underline{x}(t_n) + T_n\,f_{t_n}[\underline{x}(t_n),\underline{u}(t_n)].
$](http://www.dsprelated.com/josimages_new/pasp/img218.png){kind=small}
predicts the next state
as a function of the current state
and
current input
. In the field of computer science,
computations having this form are often called finite state
machines (or simply state machines), as they compute the
next state given the current state and external inputs.
This is a simple example of numerical integration for solving
an ODE, where in this case the ODE is given by Eq.
(1.6) (a very
general, potentially nonlinear, vector ODE). Note that the initial
state
is required to start Eq.(1.7) at time zero;
the initial state thus provides boundary conditions for the ODE at
time zero. The time sampling interval 
may be fixed for all
time as 
(as it normally is in linear, time-invariant
digital signal processing systems), or it may vary adaptively
according to how fast the system is changing (as is often needed for
nonlinear and/or time-varying systems). Further discussion of
nonlinear ODE solvers is taken up in §7.4, but for most of
this book, linear, time-invariant systems will be emphasized.
Note that for handling switching states (such as op-amp
comparators and the like), the discrete-time state-space formulation
of Eq.(1.7) is more conveniently applicable than the
continuous-time formulation in Eq.(1.6).
Next Section:
State Definition
Previous Section:
State-Space Model of a Force-Driven Mass
