Outline

In this chapter, we will look at a variety of ways to digitize macroscopic point-to-point transfer functions corresponding to a desired impulse response :

1. Sampling 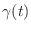to get
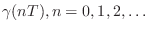
2. Pole mappings (such as 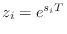followed by Prony's method)
3. Modal expansion
4. Frequency-response matching using digital filter design methods

Next, we'll look at the more specialized technique known as commuted synthesis, in which computational efficiency may be greatly increased by interchanging (``commuting'') the series order of component transfer functions. Commuted synthesis delivers large gains in efficiency for systems with a short excitation and high-order resonators, such plucked and struck strings. In Chapter 9, commuted synthesis is applied to piano modeling.

Extracting the least-damped modes of a transfer function for separate parametric implementation is often used in commuted synthesis. We look at a number of ways to accomplish this goal toward the end of this chapter.

We close the chapter with a simple example of transfer-function modeling applied to the digital phase shifter audio effect. This example classifies as virtual analog modeling, in which a valued analog device is converted to digital form in a way that preserves all valued features of the original. Further examples of transfer-function models appear in Chapter 9.

Sign in