DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Passive One-Ports

It is well known that the impedance of every passive one-port is positive real (see §C.11.2). The reciprocal of a positive real function is positive real, so every passive impedance corresponds also to a passive admittance.

A complex-valued function of a complex variable $ \Gamma (s)$ is said to be positive real (PR) if

1)
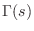$ \Gamma (s)$ is real whenever $ s$ is real
2)
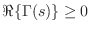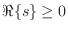$ \Re\{\Gamma(s)\} \geq 0$ whenever $ \Re\{s\} \geq 0$.

A particularly important property of positive real functions is that the phase is bounded between plus and minus $ 90$ degrees, i.e.,

$\displaystyle -\frac{\pi}{2} \leq \angle{\Gamma(j\omega)} \leq \frac{\pi}{2} $

This is a significant constraint on the rational function $ \Gamma (s)$. One implication is that in the lossless case (no dashpots, only masses and springs--a reactance) all poles and zeros interlace along the $ j\omega $ axis, as depicted in Fig.7.14.

Figure 7.14: Poles and zeros of a lossless immittance (reactance or suseptance) must interlace along the $ j\omega $ Axis. Left: Pole-zero plot. Right: Phase response. The ``spring/mass'' labels along the frequency axis correspond to the case of a lossless admittance (susceptance) in which a spring admittance ( $ \Gamma _k(j\omega )=j\omega /k$) gives a $ +\pi /2$ phase shift, while that of a mass ( $ \Gamma _m(j\omega )=-j/(m\omega )$) gives a $ -\pi /2$ phase shift between the input driving-force and output velocity.
\includegraphics[width=\twidth]{eps/interlace}

Referring to Fig.7.14, consider the graphical method for computing phase response of a reactance from the pole zero diagram [449].8.4Each zero on the positive $ j\omega $ axis contributes a net 90 degrees of phase at frequencies above the zero. As frequency crosses the zero going up, there is a switch from $ -90$ to $ +90$ degrees. For each pole, the phase contribution switches from $ +90$ to $ -90$ degrees as it is passed going up in frequency. In order to keep phase in $ [-\pi/2,\pi/2]$, it is clear that the poles and zeros must strictly alternate. Moreover, all poles and zeros must be simple, since a multiple poles or zero would swing the phase by more than $ 180$ degrees, and the reactance could not be positive real.

The positive real property is fundamental to passive immittances and comes up often in the study of measured resonant systems. A practical modeling example (passive digital modeling of a guitar bridge) is discussed in §9.2.1.

Next Section:
Finite Difference Approximation
Previous Section:
General One-Ports