Free Books
   Free Books    Physical Audio Signal Processing  

Passive Reflectance Synthesis--Method 1

The first method is based on constructing a passive reflectance $ \hat{\rho}(z)$ having the desired poles, and then converting to an admittance via the fundamental relation

$\displaystyle \Gamma(z) = \Gamma_0 \frac{1-\hat{\rho}(z)}{1+\hat{\rho}(z)} $

where $ \Gamma_0$ is an arbitrary real, positive number which can be interpreted as the wave admittance of the string on which waves enter and return from the bridge.

As we saw in §C.11.1, every passive impedance corresponds to a passive reflectance which is a Schur function (stable and having gain not exceeding $ 1$ around the unit circle). Since damping is light in a guitar bridge impedance (otherwise the strings would not vibrate very long, and sustain is a highly prized feature of real guitars), we can expect the bridge reflectance to be close to an allpass transfer function $ H_A(z)$.

It is well known that every allpass transfer function can be expressed as

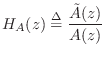
$\displaystyle H_A(z) \isdef \frac{\tilde{A}(z)}{A(z)} $

where

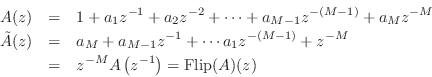
\begin{eqnarray*} A(z) &=& 1 + a_1 z^{-1} + a_2 z^{-2} + \cdots + a_{M-1} z^{-(M... ... z^{-M} \\ &=& z^{-M} A\left(z^{-1}\right) = \mbox{Flip}(A)(z) \end{eqnarray*}

We will then construct a Schur function as

$\displaystyle \hat{\rho}(z) = g H_A(z) F(z), \quad 0 < g < 1 $

where $ F(z) = f_0 + f_1(z+z^{-1}) + f_2(z^2 + z^{-2} + \cdots + f_N(z^N + z^{-N})$ is a zero-phase FIR filter which can be used to adjust peak heights without altering phase.10.6 We require $ \angle F(e^{j\omega T})=0$ which means its frequency response is real and positive. Note that being a symmetric FIR filter is not sufficient; there also can be no zero-crossings in the frequency response, which tends to limit how far the impedance magnitudes can be shaped. (For simplicity, feel free to forget about $ F(z)$ and accept that all the admittance resonances will be constrained to the same height. The second method is easier anyway.)

Recall that in every allpass filter with real coefficients, to every pole at radius $ R_i$ there corresponds a zero at radius $ 1/R_i$.10.7

Because the impedance is lightly damped, the poles and zeros of the corresponding reflectance are close to the unit circle. This means that at points along the unit circle between the poles, the poles and zeros tend to cancel. It can be easily seen using the graphical method for computing the phase of the frequency response that the pole-zero angles in the allpass filter are very close to the resonance frequencies in the corresponding passive impedance [429]. Furthermore, the distance of the allpass poles to the unit circle controls the bandwidth of the impedance peaks. Therefore, to a first approximation, we can treat the allpass pole-angles as the same as those of the impedance pole angles, and the pole radii in the allpass can be set to give the desired impedance peak bandwidth. The zero-phase shaping filter $ F(z)$ gives the desired mode height.

From the measured peak frequencies $ F_i$ and bandwidths $ B_i$ in the guitar bridge admittance, we may approximate the pole locations $ z_i = R_i e^{j\theta_i}$ as

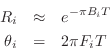
\begin{eqnarray*} R_i &\approx& e^{-\pi B_i T} \\ \theta_i &=& 2\pi F_i T \end{eqnarray*}

where $ T$ is the sampling interval as usual. Next we construct the allpass denominator as the product of elementary second-order sections:

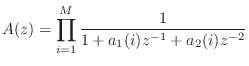
$\displaystyle A(z) = \prod_{i=1}^M \frac{1}{1 + a_1(i) z^{-1} + a_2(i) z^{-2}} $

where

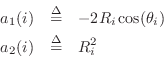
\begin{eqnarray*} a_1(i) &\isdef & -2R_i\cos(\theta_i)\\ a_2(i) &\isdef & R_i^2 \end{eqnarray*}

Now that we've constructed a Schur function, a passive admittance can be computed using (9.2.1). While it is guaranteed to be positive real, the modal frequencies, bandwidths, and amplitudes are only indirectly controlled and therefore approximated. (Of course, this would provide a good initial guess for an iterative procedure which computes an optimal approximation directly.)

A simple example of a synthetic bridge constructed using this method with $ F(z)=1$ and $ g=0.9$ is shown in Fig.9.10.

Figure 9.10: Synthetic guitar-bridge admittance using method 1.
\includegraphics[width=\twidth]{eps/lguitarsynth}

Next Section:
Passive Reflectance Synthesis--Method 2
Previous Section:
Building a Synthetic Guitar Bridge Admittance