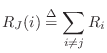DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Physical Derivation of Series Reflection Coefficient

Physically, the force-wave reflection coefficient seen at port $ i$ of a series adaptor is due to an impedance step from $ R_i$, that of the port interface, to a new impedance consisting of the series combination of all other port impedances meeting at the junction. Let

$\displaystyle R_J(i) \isdef \sum_{i\neq j} R_i \protect$ (F.35)

denote this series combination. Then we must have, as in Eq.$ \,$(F.25),

$\displaystyle \rho_i = \frac{R_J(i)-R_i}{R_J(i)+R_i}$ (F.36)

Let's check this ``physical'' derivation against the formal definition Eq.$ \,$(F.31) leading to $ \rho^v_i = \beta_i - 1$ in Eq.$ \,$(F.33). Define the total junction impedance as

$\displaystyle R_J \isdef \sum_{j=1}^N R_j $

This is the series combination of all impedances connected to the junction. Then by Eq.$ \,$(F.35), $ R_J = R_i + R_J(i)$ for all $ i$. From Eq.$ \,$(F.26), the velocity reflection coefficient is given by

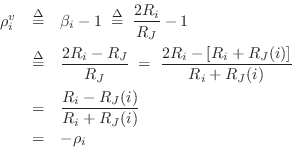
\begin{eqnarray*} \rho^v_i &\isdef & \beta_i - 1 \;\isdef \; \frac{2R_i}{R_J} -... ..._J(i)}\\ &=& \frac{R_i - R_J(i)}{R_i + R_J(i)}\\ &=& -\rho_i \end{eqnarray*}

Since

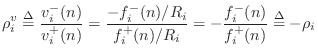
$\displaystyle \rho^v_i\isdef \frac{v^{-}_i(n)}{v^{+}_i(n)} = \frac{-f^{{-}}_i(n)/R_i}{f^{{+}}_i(n)/R_i} = - \frac{f^{{-}}_i(n)}{f^{{+}}_i(n)} \isdef -\rho_i $

the result follows.

Next Section:
Series Reflection Free Port
Previous Section:
Reflection Coefficient, Series Case