DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Poles at $ s=0$

We know from the above that the denominator of the cone reflectance has at least one root at $ s=0$. In this subsection we investigate this ``dc behavior'' of the cone more thoroughly.

A hasty analysis based on the reflection and transmission filters in Equations (C.154) and (C.155) might conclude that the reflectance of the conical cap converges to $ -1$ at dc, since $ R(0)=-1$ and $ T(0)=0$. However, this would be incorrect. Instead, it is necessary to take the limit as $ \omega\to0$ of the complete conical cap reflectance $ R_J(s)$:

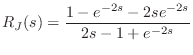$\displaystyle R_J(s) = \frac{1 - e^{-2s} - 2s e^{-2s}}{2s - 1 + e^{-2s}}$ (C.165)

We already discovered a root at $ s=0$ in the denominator in the context of the preceding stability proof. However, note that the numerator also goes to zero at $ s=0$. This indicates a pole-zero cancellation at dc. To find the reflectance at dc, we may use L'Hospital's rule to obtain

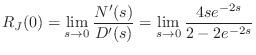$\displaystyle R_J(0) = \lim_{s\to0} \frac{N^\prime(s)}{D^\prime(s)} = \lim_{s\to 0}\frac{4s e^{-2s}}{2-2e^{-2s}}$ (C.166)

and once again the limit is an indeterminate $ 0/0$ form. We therefore apply L'Hospital's rule again to obtain

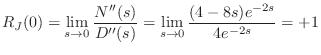$\displaystyle R_J(0) = \lim_{s\to0} \frac{N^{\prime\prime}(s)}{D^{\prime\prime}(s)} = \lim_{s\to 0}\frac{(4-8s) e^{-2s}}{4e^{-2s}} = +1$ (C.167)

Thus, two poles and zeros cancel at dc, and the dc reflectance is $ +1$, not $ -1$ as an analysis based only on the scattering filters would indicate. From a physical point of view, it makes more sense that the cone should ``look like'' a simple rigid termination of the cylinder at dc, since its length becomes small compared with the wavelength in the limit.

Another method of showing this result is to form a Taylor series expansion of the numerator and denominator:

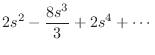$\displaystyle N(s)$ $\displaystyle =$ $\displaystyle 2 {s^2} - {{8 {s^3}}\over 3} + 2 {s^4} + \cdots$ (C.168)
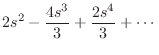$\displaystyle D(s)$ $\displaystyle =$ $\displaystyle 2 {s^2} - {{4 {s^3}}\over 3} + {{2 {s^4}}\over 3} + \cdots$ (C.169)

Both series begin with the term $ 2s^2$ which means both the numerator and denominator have two roots at $ s=0$. Hence, again the conclusion is two pole-zero cancellations at dc. The series for the conical cap reflectance can be shown to be

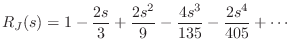$\displaystyle R_J(s) = 1 - {{2 s}\over 3} + {{2 {s^2}}\over 9} - {{4 {s^3}}\over {135}} - {{2 {s^4}}\over {405}} + \cdots$ (C.170)

which approaches $ +1$ as $ s\to0$.

An alternative analysis of this issue is given by Benade in [37].

Next Section:
A Class of Well Posed Damped PDEs
Previous Section:
Reflectance Magnitude