Practical Advice
In summary, the following pointers can be offered regarding nonlinear elements in a digital waveguide model:
- Verify that aliasing can be heard and sounds bad before working
to get rid of it.
- Aliasing (bandwidth expansion) is reduced by smoothing
``corners'' in the nonlinearity.
- Consider an oversampling factor for nonlinear
subsystems sufficient to accommodate the bandwidth expansion
caused by the nonlinearity.
- Make sure there is adequate lowpass filtering in a feedback loop
containing a nonlinearity.
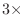 oversampling, and
oversampling, and
- a lowpass filter to
![$ \omega\in[-\pi/3,\pi/3]$](http://www.dsprelated.com/josimages_new/pasp/img1557.png) after the nonlinearity.
after the nonlinearity.
Another variation is to oversample by two, in which case there is aliasing, but that aliasing does not reach the ``base band.'' Therefore, a half-band lowpass filter rejects both the second spectral image and the third, which is aliased onto the second.
Next Section:
FDA in the Frequency Domain
Previous Section:
Stability of Nonlinear Feedback Loops




















