Free Books
   Free Books    Physical Audio Signal Processing  

Reactive Terminations

In typical string models for virtual musical instruments, the ``nut end'' of the string is rigidly clamped while the ``bridge end'' is terminated in a passive reflectance $ S(z)$. The condition for passivity of the reflectance is simply that its gain be bounded by 1 at all frequencies [447]:

$\displaystyle \left\vert S(e^{j\omega T})\right\vert\leq 1, \quad \forall\, \omega T\in[-\pi,\pi). \protect$ (E.42)

A very simple case, used, for example, in the Karplus-Strong plucked-string algorithm, is the two-point-average filter:

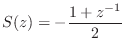
$\displaystyle S(z) = -\frac{1+z^{-1}}{2} $

To impose this lowpass-filtered reflectance on the right in the chosen subgrid, we may form

   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathbf{A}}$}$$\displaystyle _W=$   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}$$\displaystyle _W- \frac{1}{2}{\bm \Delta}_{8,5} - \frac{1}{2}{\bm \Delta}_{8,7} $

which results in the FDTD transition matrix
\begin{eqnarray*} \mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathb... ... \\ 0 & 0 & 0 & 0 & -1/2 & 1/2 & -1 & -1 \end{array}\!\right]. \end{eqnarray*}
This gives the desired filter in a half-rate, staggered grid case. In the full-rate case, the termination filter is really

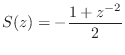
$\displaystyle S(z) = -\frac{1+z^{-2}}{2} $

which is still passive, since it obeys Eq.$ \,$(E.42), but it does not have the desired amplitude response: Instead, it has a notch (gain of 0) at one-fourth the sampling rate, and the gain comes back up to 1 at half the sampling rate. In a full-rate scheme, the two-point-average filter must straddle both subgrids. Another often-used string termination filter in digital waveguide models is specified by [447]
\begin{eqnarray*} s(n) &=& -g\left[\frac{h}{4}, \frac{1}{2}, \frac{h}{4}\right]\... ...{j\omega T})&=& -e^{-j\omega T}g\frac{1 + h \cos(\omega T)}{2}, \end{eqnarray*}
where $ g\in(0,1)$ is an overall gain factor that affects the decay rate of all frequencies equally, while $ h\in(0,1)$ controls the relative decay rate of low-frequencies and high frequencies. An advantage of this termination filter is that the delay is always one sample, for all frequencies and for all parameter settings; as a result, the tuning of the string is invariant with respect to termination filtering. In this case, the perturbation is

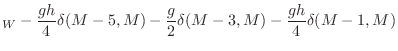
   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathbf{A}}$}$$\displaystyle _W=$   $\displaystyle \mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}$$\displaystyle _W- \frac{gh}{4}\delta(M-5,M) - \frac{g}{2}\delta(M-3,M) - \frac{gh}{4}\delta(M-1,M) $

and, using Eq.$ \,$(E.41), the order $ M=8$ FDTD state transition matrix is given by
\begin{eqnarray*} \mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathb... ...d g_2 & \quad -g_2 & \quad g_3 & \quad -g_3 \end{array}\!\right] \end{eqnarray*}
where
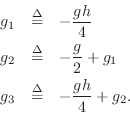
\begin{eqnarray*} g_1 &\isdef & -\frac{gh}{4}\\ g_2 &\isdef & -\frac{g}{2}+g_1\\ g_3 &\isdef & -\frac{gh}{4}+g_2.\\ \end{eqnarray*}
The filtered termination examples of this section generalize immediately to arbitrary finite-impulse response (FIR) termination filters $ S(z)$. Denote the impulse response of the termination filter by

$\displaystyle s(n)=[s_0,s_1,s_2,\ldots,s_N], $

where the length $ N$ of the filter does not exceed $ M/2$. Due to the DW-FDTD equivalence, the general stability condition is stated very simply as

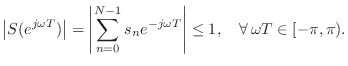
$\displaystyle \left\vert S(e^{j\omega T})\right\vert = \left\vert\sum_{n=0}^{N-1} s_n e^{-j\omega T}\right\vert \leq 1, \quad \forall\, \omega T\in[-\pi,\pi). $

Next Section:
Interior Scattering Junctions
Previous Section:
Boundary Conditions as Perturbations