DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Reflectance of the Conical Cap

Let $ {t_{\xi}}\isdef \xi/c$ denote the time to propagate across the length of the cone in one direction. As is well known [22], the reflectance at the tip of an infinite cone is $ -1$ for pressure waves. I.e., it reflects like an open-ended cylinder. We ignore any absorption losses propagating in the cone, so that the transfer function from the entrance of the cone to the tip is $ e^{-s{t_{\xi}}}$. Similarly, the transfer function from the conical tip back to the entrance is also $ e^{-s{t_{\xi}}}$. The complete reflection transfer function from the entrance to the tip and back is then

$\displaystyle R_{t_{\xi}}(s) = - e^{-2s{t_{\xi}}}$ (C.155)

Note that this is the reflectance a distance $ \xi=c{t_{\xi}}$ from a conical tip inside the cone.

We now want to interface the conical cap reflectance $ R_{t_{\xi}}(s)$ to the cylinder. Since this entails a change in taper angle, there will be reflection and transmission filtering at the cylinder-cone junction given by Eq.$ \,$(C.154) and Eq.$ \,$(C.155).

From inside the cylinder, immediately next to the cylinder-cone junction shown in Fig.C.48, the reflectance of the conical cap is readily derived from Fig.C.48b and Equations (C.154) and (C.155) to be

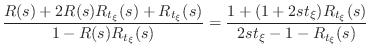$\displaystyle R_J(s)$ $\displaystyle =$ $\displaystyle \frac{R(s) + 2 R(s) R_{t_{\xi}}(s) + R_{t_{\xi}}(s)}{1 - R(s)R_{t... ...}}(s)} = \frac{1 + (1+2s{t_{\xi}})R_{t_{\xi}}(s)}{2s{t_{\xi}}-1-R_{t_{\xi}}(s)}$  
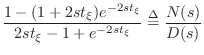  $\displaystyle =$ $\displaystyle \frac{1 - (1+2s{t_{\xi}})e^{-2s{t_{\xi}}}}{2s{t_{\xi}}-1+e^{-2s{t_{\xi}}}} \isdef \frac{N(s)}{D(s)}$ (C.156)

where

$\displaystyle N(s) \isdef 1 - e^{-2s{t_{\xi}}} - 2s{t_{\xi}}e^{-2s{t_{\xi}}}$ (C.157)

is the numerator of the conical cap reflectance, and

$\displaystyle D(s) \isdef 2 s{t_{\xi}}- 1 + e^{-2s{t_{\xi}}}$ (C.158)

is the denominator. Note that for very large $ {t_{\xi}}$, the conical cap reflectance approaches $ R_J = -e^{-2s{t_{\xi}}}$ which coincides with the impedance of a length $ \xi=c{t_{\xi}}$ open-end cylinder, as expected.

Next Section:
Stability Proof
Previous Section:
Scattering Filters at the Cylinder-Cone Junction