Free Books
   Free Books    Physical Audio Signal Processing  

Reflection and Refraction

The first equality in Eq.$ \,$(C.56) implies that the angle of incidence equals angle of reflection:

$\displaystyle \zbox {\theta_1^+=\theta_1^-} % \isdef\theta_1} $

We now wish to find the wavenumber in medium 2. Let $ c_i$ denote the phase velocity in wave impedance $ R_i$:

$\displaystyle c_i = \frac{\omega}{k_i}, \quad i=1,2 $

In impedance $ R_2$, we have in particular

$\displaystyle \omega^2 \eqsp c_2^2 k_2^2 \eqsp c_2^2 \left[(k^+_{2x})^2 + (k^+_{2y})^2\right]. $

Solving for $ k^+_{2x}$ gives

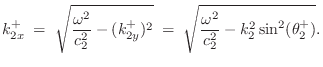
$\displaystyle k^+_{2x} \eqsp \sqrt{\frac{\omega^2}{c_2^2} - (k^+_{2y})^2} \eqsp \sqrt{\frac{\omega^2}{c_2^2} - k_2^2\sin^2(\theta_2^+)}. $

Since $ k_1\sin(\theta_1^+)=k_2\sin(\theta_2^+)$ from above,

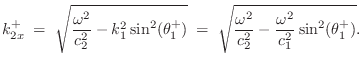
$\displaystyle k^+_{2x} \eqsp \sqrt{\frac{\omega^2}{c_2^2} - k_1^2\sin^2(\theta... ...\eqsp \sqrt{\frac{\omega^2}{c_2^2}-\frac{\omega^2}{c_1^2}\sin^2(\theta_1^+)}. $

We have thus derived

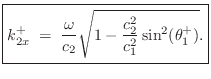
$\displaystyle \zbox {k^+_{2x} \eqsp \frac{\omega}{c_2}\sqrt{1 - \frac{c_2^2}{c_1^2}\sin^2(\theta_1^+)}.} $

We earlier established $ k^+_{2y} = k^+_{1y}$ (for agreement along the boundary, by pressure continuity). This describes the refraction of the plane wave as it passes through the impedance-change boundary. The refraction angle depends on ratio of phase velocities $ c_2/c_1$. This ratio is often called the index of refraction:

$\displaystyle n \isdef \frac{c_2}{c_1} $

and the relation $ k_1\sin(\theta_1^+)=k_2\sin(\theta_2^+)$ is called Snell's Law (of refraction).

Next Section:
Evanescent Wave due to Total Internal Reflection
Previous Section:
Reflection Coefficient