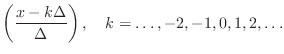Free Books
   Free Books    Physical Audio Signal Processing  

Relation of Lagrange to Sinc Interpolation

For an infinite number of equally spaced samples, with spacing $ x_{k+1}-x_k = \Delta$, the Lagrangian basis polynomials converge to shifts of the sinc function, i.e.,

$\displaystyle l_k(x) =$   sinc$\displaystyle \left(\frac{x-k\Delta}{\Delta}\right), \quad k=\ldots,-2,-1,0,1,2,\ldots $

where

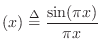
   sinc$\displaystyle (x) \isdef \frac{\sin(\pi x)}{\pi x} $

A simple argument is based on the fact that any analytic function is determined by its zeros and its value at one point. Since sinc$ (x)$ is zero on all the integers except 0, and since sinc$ (0)=1$, it must coincide with the infinite-order Lagrangian basis polynomial for the sample at $ x=0$ which also has its zeros on the nonzero integers and equals $ 1$ at $ x=0$. The equivalence of sinc interpolation to Lagrange interpolation was apparently first published by the mathematician Borel in 1899, and has been rediscovered many times since [309, p. 325]. A direct proof can be based on the equivalance between Lagrange interpolation and windowed-sinc interpolation using a ``scaled binomial window'' [262,502]. That is, for a fractional sample delay of $ D$ samples, multiply the shifted-by-$ D$, sampled, sinc function

$\displaystyle h_s(n) =$   sinc$\displaystyle (n-D) = \frac{\sin[\pi(n-D)]}{\pi(n-D)} $

by a binomial window

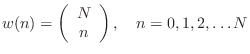
$\displaystyle w(n) = \left(\begin{array}{c}N\\ n\end{array}\right), \quad n=0,1,2,\ldots N $

and normalize by [502]

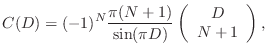
$\displaystyle C(D) = (-1)^N\frac{\pi(N+1)}{\sin(\pi D)}\left(\begin{array}{c}D\\ N+1\end{array}\right), $

which scales the interpolating filter to have a unit $ L_2$ norm, to obtain the $ N$th-order Lagrange interpolating filter

$\displaystyle h_D(n)=C(D)w(n)h_s(n), \quad n=0,1,2,\ldots,N $

Since the binomial window converges to the Gaussian window as $ N\to\infty$, and since the window gets wider and wider, approaching a unit constant in the limit, the convergence of Lagrange to sinc interpolation can be seen. A more recent alternate proof appears in [557].
Next Section:
Thiran Allpass Interpolation in Matlab
Previous Section:
Recent Developments in Lagrange Interpolation