The Reverberation Problem
Consider the requirements for acoustically simulating a concert hall or other listening space. Suppose we only need the response at one or more discrete listening points in space (``ears'') due to one or more discrete point sources of acoustic energy.
First, as discussed in §2.2, the direct signal
propagating from a sound source to a listener's ear can be simulated
using a single delay line in series with an attenuation scaling or
lowpass filter. Second, each sound ray arriving at the listening
point via one or more reflections can be simulated using a
delay-line and some scale factor (or filter). Two rays create a
feedforward comb filter, like the one in Fig.2.9 on
page ![]() . More generally, a tapped delay line
(Fig.2.19) can simulate many reflections. Each tap brings out one
echo at the appropriate delay and gain, and each tap can be
independently filtered to simulate air absorption and lossy
reflections. In principle, tapped delay lines can accurately simulate
any reverberant environment, because reverberation really does
consist of many paths of acoustic propagation from each source to each
listening point. As we will see, the only limitations of a tapped
delay line are (1) it is expensive computationally relative to
other techniques, (2) it handles only one ``point to point'' transfer
function, i.e., from one point-source to one ear,4.1 and (3) it should be changed when the source,
listener, or anything in the room moves.
. More generally, a tapped delay line
(Fig.2.19) can simulate many reflections. Each tap brings out one
echo at the appropriate delay and gain, and each tap can be
independently filtered to simulate air absorption and lossy
reflections. In principle, tapped delay lines can accurately simulate
any reverberant environment, because reverberation really does
consist of many paths of acoustic propagation from each source to each
listening point. As we will see, the only limitations of a tapped
delay line are (1) it is expensive computationally relative to
other techniques, (2) it handles only one ``point to point'' transfer
function, i.e., from one point-source to one ear,4.1 and (3) it should be changed when the source,
listener, or anything in the room moves.
Exact Reverb via Transfer-Function Modeling
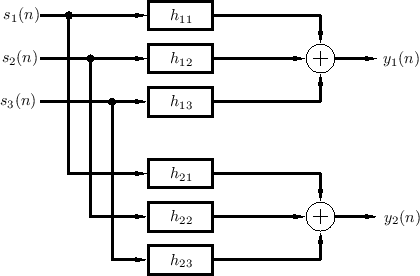
Figure 3.1 depicts the general reverberation scenario for three sources and one listener (two ears). In general, the filters should also include filtering by the pinnae of the ears, so that each echo can be perceived as coming from the correct angle of arrival in 3D space; in other words, at least some reverberant reflections should be spatialized so that they appear to come from their natural directions in 3D space [248]. Again, the filters change if anything changes in the listening space, including source or listener position. The artificial reverberation problem is then to implement some approximation of the system in Fig.3.1.
 |
In the frequency domain, it is convenient to express the input-output relationship in terms of the transfer-function matrix:
![$\displaystyle \left[\begin{array}{c} Y_1(z) \\ [2pt] Y_2(z) \end{array}\right] ...
...left[\begin{array}{c} S_1(z) \\ [2pt] S_2(z) \\ [2pt] S_3(z)\end{array}\right]
$](http://www.dsprelated.com/josimages_new/pasp/img663.png)
Denoting the impulse response of the filter from source ![]() to ear
to ear ![]() by
by ![]() , the two output signals in Fig.3.1 are computed by
six convolutions:
, the two output signals in Fig.3.1 are computed by
six convolutions:
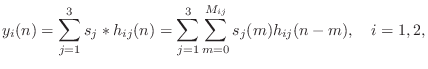
Complexity of Exact Reverberation
For music, a typical reverberation time4.2is on the order of one second. Suppose we choose exactly one second for the reverberation time. At an audio sampling rate of 50 kHz, each filter in Fig.3.1 requires 50,000 multiplies and additions per sample, or 2.5 billion multiply-adds per second. Handling three sources and two listening points (ears), we reach 30 billion operations per second for the reverberator. This computational load would require at least 10 Pentium CPUs clocked at 3 Gigahertz, assuming they were doing nothing else, and assuming both a multiply and addition can be initiated each clock cycle, with no wait-states caused by the three required memory accesses (input, output, and filter coefficient). While these numbers can be improved using FFT convolution instead of direct convolution (at the price of introducing a throughput delay which can be a problem for real-time systems), it remains the case that exact implementation of all relevant point-to-point transfer functions in a reverberant space is very expensive computationally.
While a tapped delay line FIR filter can provide an accurate model for any point-to-point transfer function in a reverberant environment, it is rarely used for this purpose in practice because of the extremely high computational expense. While there are specialized commercial products that implement reverberation via direct convolution of the input signal with the impulse response, the great majority of artificial reverberation systems use other methods to synthesize the late reverb more economically.
Possibility of a Physical Reverb Model
One disadvantage of the point-to-point transfer function model depicted in Fig.3.1 is that some or all of the filters must change when anything moves. If instead we had a computational model of the whole acoustic space, sources and listeners could be moved as desired without affecting the underlying room simulation. Furthermore, we could use ``virtual dummy heads'' as listeners, complete with pinnae filters, so that all of the 3D directional aspects of reverberation could be captured in two extracted signals for the ears. Thus, there are compelling reasons to consider a full 3D model of a desired acoustic listening space.
Let us briefly estimate the computational requirements of a ``brute force'' acoustic simulation of a room. It is generally accepted that audio signals require a 20 kHz bandwidth. Since sound travels at about a foot per millisecond (see §B.7.14 for a more precise value), a 20 kHz sinusoid has a wavelength on the order of 1/20 feet, or about half an inch. Since, by elementary sampling theory, we must sample faster than twice the highest frequency present in the signal, we need ``grid points'' in our simulation separated by a quarter inch or less. At this grid density, simulating an ordinary 12'x12'x8' room in a home requires more than 100 million grid points. Using finite-difference (Appendix D) or waveguide-mesh techniques (§C.14,Appendix E) [518,396], the average grid point can be implemented as a multiply-free computation; however, since it has waves coming and going in six spatial directions, it requires on the order of 10 additions per sample. Thus, running such a room simulator at an audio sampling rate of 50 kHz requires on the order of 50 billion additions per second, which is comparable to the three-source, two-ear simulation of Fig.3.1. However, scaling up to a 100'x50'x20' concert hall requires more than 5 quadrillion operations per second. We may conclude, therefore, that a fine-grained physical model of a complete concert hall over the audio band is prohibitively expensive.
The remainder of this chapter will be concerned with ways of reducing computational complexity without sacrificing too much perceptual quality.
Next Section:
Perceptual Aspects of Reverberation
Previous Section:
Allpass Digital Waveguide Networks




















