The Second-Order Waveguide Filter
The first step is to make a second-order digital filter with zero
damping by abutting two unit-sample sections of waveguide medium, and
terminating on the left and right with perfect reflections, as shown
in Fig.C.38. The wave impedance in section ![]() is given by
is given by
![]() , where
, where ![]() is air density,
is air density, ![]() is the
cross-sectional area of tube section
is the
cross-sectional area of tube section ![]() , and
, and ![]() is sound speed. The
reflection coefficient is determined by the impedance discontinuity
via
is sound speed. The
reflection coefficient is determined by the impedance discontinuity
via
![]() . It turns out that to obtain sinusoidal
oscillation, one of the terminations must provide an inverting
reflection while the other is non-inverting.
. It turns out that to obtain sinusoidal
oscillation, one of the terminations must provide an inverting
reflection while the other is non-inverting.
![\includegraphics[width=\twidth]{eps/wgf}](http://www.dsprelated.com/josimages_new/pasp/img4129.png) |
At the junction between sections ![]() and
and ![]() , the signal is partially
transmitted and partially reflected such that energy is conserved, i.e., we
have lossless scattering. The formula for the reflection
coefficient
, the signal is partially
transmitted and partially reflected such that energy is conserved, i.e., we
have lossless scattering. The formula for the reflection
coefficient ![]() can be derived from the physical constraints that (1)
pressure is continuous across the junction, and (2) there is no net flow
into or out of the junction. For traveling pressure waves
can be derived from the physical constraints that (1)
pressure is continuous across the junction, and (2) there is no net flow
into or out of the junction. For traveling pressure waves ![]() and
volume-velocity waves
and
volume-velocity waves ![]() , we have
, we have
![]() and
and
![]() . The physical pressure and volume velocity are obtained by
summing the traveling-wave components.
. The physical pressure and volume velocity are obtained by
summing the traveling-wave components.
The discrete-time simulation for the physical system of Fig.C.38 is shown in Fig.C.39. The propagation time from the junction to a reflecting termination and back is one sample period. The half sample delay from the junction to the reflecting termination has been commuted with the termination and combined with the half sample delay to the termination. This is a special case of a ``half-rate'' waveguide filter [433].
Since only two samples of delay are present, the digital system is at most
second order, and since the coefficients are real, at most one frequency of
oscillation is possible in ![]() .
.
The scattering junction shown in the figure is called the Kelly-Lochbaum junction in the literature on lattice and ladder digital filters [173]. While it is the most natural from a physical point of view, it requires four multiplies and two additions for its implementation.
It is well known that lossless scattering junctions can be implemented in a
variety of equivalent forms, such as the two-multiply and even one-multiply
junctions. However, most have the disadvantage of not being normalized in the sense that changing the reflection coefficient ![]() changes the amplitude of oscillation. This can be understood physically by
noting that a change in
changes the amplitude of oscillation. This can be understood physically by
noting that a change in ![]() implies a change in
implies a change in ![]() . Since the
signal power contained in a waveguide variable, say
. Since the
signal power contained in a waveguide variable, say ![]() , is
, is
![]() , we find that modulating the reflection coefficient
corresponds to modulating the signal energy represented by the signal
sample in at least one of the two delay elements. Since energy is
proportional to amplitude squared, energy modulation implies amplitude
modulation.
, we find that modulating the reflection coefficient
corresponds to modulating the signal energy represented by the signal
sample in at least one of the two delay elements. Since energy is
proportional to amplitude squared, energy modulation implies amplitude
modulation.
The well-known normalization procedure is to replace the traveling
pressure waves ![]() by ``root-power'' pressure waves
by ``root-power'' pressure waves
![]() so that signal power is just the square of a signal
sample
so that signal power is just the square of a signal
sample
![]() . When this is done, the scattering junction
transforms from the Kelly-Lochbaum or one-multiply form into the
normalized ladder junction in which the reflection coefficients
are again
. When this is done, the scattering junction
transforms from the Kelly-Lochbaum or one-multiply form into the
normalized ladder junction in which the reflection coefficients
are again ![]() , but the forward and reverse transmission
coefficients become
, but the forward and reverse transmission
coefficients become
![]() . Defining
. Defining
![]() , the
transmission coefficients can be seen as
, the
transmission coefficients can be seen as
![]() , and we arrive
essentially at the coupled form, or two-dimensional vector
rotation considered in [168].
, and we arrive
essentially at the coupled form, or two-dimensional vector
rotation considered in [168].
An alternative normalization technique is based on the digital waveguide
transformer (§C.16). The purpose of a ``transformer'' is to
``step'' the force variable (pressure in our example) by some factor ![]() without scattering and without affecting signal energy. Since traveling
signal power is proportional to pressure times velocity
without scattering and without affecting signal energy. Since traveling
signal power is proportional to pressure times velocity ![]() , it
follows that velocity must be stepped by the inverse factor
, it
follows that velocity must be stepped by the inverse factor ![]() to keep
power constant. This is the familiar behavior of transformers for analog
electrical circuits: voltage is stepped up by the ``turns ratio'' and
current is stepped down by the reciprocal factor. Now, since
to keep
power constant. This is the familiar behavior of transformers for analog
electrical circuits: voltage is stepped up by the ``turns ratio'' and
current is stepped down by the reciprocal factor. Now, since
![]() , traveling signal power is equal to
, traveling signal power is equal to
![]() . Therefore,
stepping up pressure through a transformer by the factor
. Therefore,
stepping up pressure through a transformer by the factor ![]() corresponds to
stepping up the wave impedance
corresponds to
stepping up the wave impedance ![]() by the factor
by the factor ![]() . In other words,
the transformer raises pressure and decreases volume velocity by raising
the wave impedance (narrowing the acoustic tube) like a converging cone.
. In other words,
the transformer raises pressure and decreases volume velocity by raising
the wave impedance (narrowing the acoustic tube) like a converging cone.
If a transformer is inserted in a waveguide immediately to the left, say,
of a scattering junction, it can be used to modulate the wave impedance
``seen'' to the left by the junction without having to use root-power waves
in the simulation. As a result, the one-multiply junction can be used for
the scattering junction, since the junction itself is not normalized.
Since the transformer requires two multiplies, a total of three multiplies
can effectively implement a normalized junction, where four were needed
before. Finally, in just this special case, one of the transformer
coefficients can be commuted with the delay element on the left and
combined with the other transformer coefficient. For convenience, the ![]() coefficient on the left is commuted into the junction so it merely toggles
the signs of inputs to existing summers. These transformations lead to the
final form shown in Fig.C.40.
coefficient on the left is commuted into the junction so it merely toggles
the signs of inputs to existing summers. These transformations lead to the
final form shown in Fig.C.40.
The ``tuning coefficient'' is given by
![]() , where
, where
![]() is the desired oscillation frequency in Hz at sample
is the desired oscillation frequency in Hz at sample ![]() (in the
undamped case), and
(in the
undamped case), and ![]() is the sampling period in seconds. The
``amplitude coefficient'' is
is the sampling period in seconds. The
``amplitude coefficient'' is
![]() , where growth or
decay factor per sample (
, where growth or
decay factor per sample (
![]() for constant
amplitude),C.14 and
for constant
amplitude),C.14 and ![]() is the normalizing transformer ``turns
ratio'' given by
is the normalizing transformer ``turns
ratio'' given by
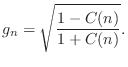
When amplitude and frequency are constant, there is no gradual exponential
growth or decay due to round-off error. This happens because the only
rounding is at the output of the tuning multiply, and all other
computations are exact. Therefore, quantization in the tuning coefficient
can only cause quantization in the frequency of oscillation. Note that any
one-multiply digital oscillator should have this property. In contrast,
the only other known normalized oscillator, the coupled form, does
exhibit exponential amplitude drift because it has two coefficients
![]() and
and
![]() which, after quantization, no longer
obey
which, after quantization, no longer
obey ![]() for most tunings.
for most tunings.
Next Section:
Application to FM Synthesis
Previous Section:
Digital Sinusoid Generators








![\includegraphics[width=\twidth]{eps/dwgf}](http://www.dsprelated.com/josimages_new/pasp/img4134.png)
![\includegraphics[scale=0.9]{eps/tnwgoAI}](http://www.dsprelated.com/josimages_new/pasp/img4149.png)












