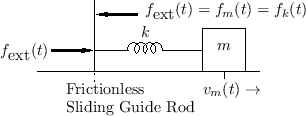
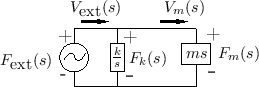Spring-Mass System
When two physical elements are driven by a common force (yet
have independent velocities, as we'll soon see is quite possible),
they are formally in parallel. An example is a mass connected
to a spring in which the driving force is applied to one end of the
spring, and the mass is attached to the other end, as shown in
Fig.7.11. The compression force on the spring
is equal at all times to the rightward force on the mass. However,
the spring compression velocity ![]() does not always equal the
mass velocity
does not always equal the
mass velocity ![]() . We do have that the sum of the mass velocity
and spring compression velocity gives the velocity of the driving point,
i.e.,
. We do have that the sum of the mass velocity
and spring compression velocity gives the velocity of the driving point,
i.e.,
![]() . Thus, in a parallel connection, forces
are equal and velocities sum.
. Thus, in a parallel connection, forces
are equal and velocities sum.
Figure 7.12 shows the electrical equivalent circuit corresponding to Fig.7.11.
 |
Next Section:
Mechanical Impedance Analysis
Previous Section:
Parallel Combination of One-Ports