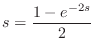Stability Proof
A transfer function
![]() is stable if there are no poles in
the right-half
is stable if there are no poles in
the right-half ![]() plane. That is, for each zero
plane. That is, for each zero ![]() of
of ![]() , we must
have
re
, we must
have
re![]() . If this can be shown, along with
. If this can be shown, along with
![]() , then the reflectance
, then the reflectance ![]() is shown to be
passive. We must also study the system zeros (roots of
is shown to be
passive. We must also study the system zeros (roots of ![]() ) in order to
determine if there are any pole-zero cancellations (common factors in
) in order to
determine if there are any pole-zero cancellations (common factors in
![]() and
and ![]() ).
).
Since
re![]() if and only if
re
if and only if
re![]() , for
, for
![]() , we may set
, we may set
![]() without loss of generality. Thus, we need only
study the roots of
without loss of generality. Thus, we need only
study the roots of
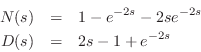
If this system is stable, we have stability also for all
![]() .
Since
.
Since ![]() is not a rational function of
is not a rational function of ![]() , the reflectance
, the reflectance ![]() may have infinitely many poles and zeros.
may have infinitely many poles and zeros.
Let's first consider the roots of the denominator
| (C.159) |
At any solution
To obtain separate equations for the real and imaginary parts, set
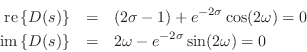
Both of these equations must hold at any pole of the reflectance. For
stability, we further require
![]() . Defining
. Defining
![]() and
and
![]() , we obtain the somewhat simpler conditions
, we obtain the somewhat simpler conditions
For any poles of ![]() on the
on the ![]() axis, we have
axis, we have ![]() , and
Eq.
, and
Eq.![]() (C.163) reduces to
(C.163) reduces to
It is well known that the ``sinc function''
We have so far proved that any poles on the ![]() axis must be at
axis must be at
![]() .
.
The same argument can be extended to the entire right-half
plane as follows. Going back to the more general case of
Eq.![]() (C.163), we have
(C.163), we have
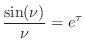 |
(C.164) |
Since
In the left-half plane, there are many potential poles.
Equation (C.162) has infinitely many solutions for each ![]() since the elementary inequality
since the elementary inequality
![]() implies
implies
![]() . Also, Eq.
. Also, Eq.![]() (C.163) has an increasing
number of solutions as
(C.163) has an increasing
number of solutions as ![]() grows more and more negative; in the limit of
grows more and more negative; in the limit of
![]() , the number of solutions is infinite and given by the roots
of
, the number of solutions is infinite and given by the roots
of ![]() (
(
![]() for any integer
for any integer ![]() ).
However, note that at
).
However, note that at
![]() , the solutions of Eq.
, the solutions of Eq.![]() (C.162) converge to the roots of
(C.162) converge to the roots of
![]() (
(
![]() for any integer
for any integer ![]() ).
The only issue is that the solutions of Eq.
).
The only issue is that the solutions of Eq.![]() (C.162) and Eq.
(C.162) and Eq.![]() (C.163)
must occur together.
(C.163)
must occur together.
![\includegraphics[width=3.5in]{eps/cylconelhp}](http://www.dsprelated.com/josimages_new/pasp/img4420.png) |
Figure C.49 plots the locus of real-part zeros (solutions to
Eq.![]() (C.162)) and imaginary-part zeros (Eq.
(C.162)) and imaginary-part zeros (Eq.![]() (C.163)) in a portion
the left-half plane. The roots at
(C.163)) in a portion
the left-half plane. The roots at ![]() can be seen at the
middle-right. Also, the asymptotic interlacing of these loci can be
seen along the left edge of the plot. It is clear that the two loci
must intersect at infinitely many points in the left-half plane near
the intersections indicated in the graph. As
can be seen at the
middle-right. Also, the asymptotic interlacing of these loci can be
seen along the left edge of the plot. It is clear that the two loci
must intersect at infinitely many points in the left-half plane near
the intersections indicated in the graph. As
![]() becomes
large, the intersections evidently converge to the peaks of the
imaginary-part root locus (a log-sinc function rotated
90 degrees). At all frequencies
becomes
large, the intersections evidently converge to the peaks of the
imaginary-part root locus (a log-sinc function rotated
90 degrees). At all frequencies ![]() , the roots occur near
the log-sinc peaks, getting closer to the peaks as
, the roots occur near
the log-sinc peaks, getting closer to the peaks as
![]() increases. The log-sinc peaks thus provide a reasonable estimate
number and distribution in the left-half
increases. The log-sinc peaks thus provide a reasonable estimate
number and distribution in the left-half ![]() -plane. An outline of an
analytic proof is as follows:
-plane. An outline of an
analytic proof is as follows:
- Rotate the loci in Fig.C.49 counterclockwise by 90 degrees.
- Prove that the two root loci are continuous, single-valued functions of
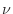 (as the figure suggests).
(as the figure suggests).
- Prove that for
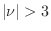 , there are infinitely many extrema
of the log-sinc function (imaginary-part root-locus) which have
negative curvature and which lie below
, there are infinitely many extrema
of the log-sinc function (imaginary-part root-locus) which have
negative curvature and which lie below 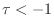 (as the figure
suggests). The
(as the figure
suggests). The 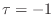 and
and 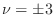 lines are shown in the
figure as dotted lines.
lines are shown in the
figure as dotted lines.
- Prove that the other root locus (for the real part) has
infinitely many similar extrema which occur for
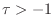 (again as
the figure suggests).
(again as
the figure suggests).
- Prove that the two root-loci interlace at
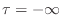 (already done above).
(already done above).
- Then topologically, the continuous functions must cross at
infinitely many points in order to achieve interlacing at
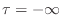 .
.
The peaks of the log-sinc function not only indicate approximately where the left-half-plane roots occur
Next Section:
Reflectance Magnitude
Previous Section:
Reflectance of the Conical Cap