Striking the Rod in the Middle
First, consider
![]() . That is, we apply an
upward unit-force impulse at time 0 in the middle of the rod. The
total momentum delivered in the neighborhood of
. That is, we apply an
upward unit-force impulse at time 0 in the middle of the rod. The
total momentum delivered in the neighborhood of ![]() and
and ![]() is
obtained by integrating the applied force density with respect to time
and position:
is
obtained by integrating the applied force density with respect to time
and position:
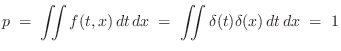
The kinetic energy of the system after time zero is
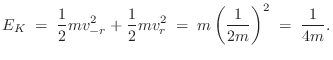
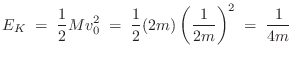
Next Section:
Striking One of the Masses
Previous Section:
Circular Cross-Section




















