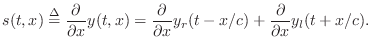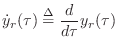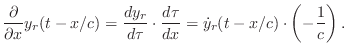String Slope from Velocity Waves

Let's use the above result to derive the slope of the ideal vibrating string From Eq. $\,$ (C.11), we have the string displacement given by

$\displaystyle y(t,x) = y_r(t-x/c) + y_l(t+x/c). \protect$

By linearity of differentiation, the string slope is given by

$\displaystyle s(t,x) \isdef \frac{\partial}{\partial x} y(t,x) = \frac{\partial}{\partial x}y_r(t-x/c) + \frac{\partial}{\partial x}y_l(t+x/c).$

Consider only the right-going component, and define

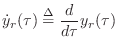
$\displaystyle {\dot y}_r(\tau) \isdef \frac{d}{d\tau} y_r(\tau)$

with $\tau\isdef t-x/c$ . By the chain rule,

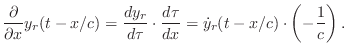
$\displaystyle \frac{\partial}{\partial x}y_r(t-x/c) = \frac{dy_r}{d\tau} \cdot \frac{d\tau}{dx} = {\dot y}_r(t-x/c)\cdot\left(-\frac{1}{c}\right).$

The left-going component is similar, but with

. Thus, the string slope in terms of traveling velocity-wave components can be written as

$\displaystyle s(t,x) = \frac{1}{c}{\dot y}_l(t+x/c) - \frac{1}{c}{\dot y}_r(t-x/c).$

Next Section:
Wave Velocity
Previous Section:
Use of the Chain Rule

Sign in