Summary of Lumped Modeling
In this chapter, we looked at the fundamentals of lumped modeling elements such as masses, springs, and dashpots. The important concept of driving-point impedance was defined and discussed, and electrical equivalent circuits were developed, along with associated elementary (circuit) network theory. Finally, we looked at basic ways of digitizing lumped elements and more complex ODEs and PDEs, including a first glance at some nonlinear methods.
Practical examples of lumped models begin in §9.3.1. In particular, piano-like models require a ``hammer'' to strike the string, and §9.3.1 explicates the simplest case of an ideal point-mass striking an ideal vibrating string. In that model, when the mass is in contact with the string, it creates a scattering junction on the string having reflection and transmission coefficients that are first-order filters. These filters are then digitized via the bilinear transform. The ideal string itself is of course modeled as a digital waveguide. A detailed development of wave scattering at impedance-discontinuities is presented for digital waveguide models in §C.8, and for wave digital filters in Appendix F.
Outline
In this chapter, we will look at a variety of ways to digitize
macroscopic point-to-point transfer functions ![]() corresponding to a desired impulse response
corresponding to a desired impulse response ![]() :
:
- Sampling
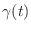 to get
to get
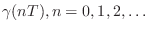
- Pole mappings (such as
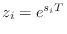 followed by Prony's method)
followed by Prony's method)
- Modal expansion
- Frequency-response matching using digital filter design methods
Next, we'll look at the more specialized technique known as commuted synthesis, in which computational efficiency may be greatly increased by interchanging (``commuting'') the series order of component transfer functions. Commuted synthesis delivers large gains in efficiency for systems with a short excitation and high-order resonators, such plucked and struck strings. In Chapter 9, commuted synthesis is applied to piano modeling.
Extracting the least-damped modes of a transfer function for separate parametric implementation is often used in commuted synthesis. We look at a number of ways to accomplish this goal toward the end of this chapter.
We close the chapter with a simple example of transfer-function modeling applied to the digital phase shifter audio effect. This example classifies as virtual analog modeling, in which a valued analog device is converted to digital form in a way that preserves all valued features of the original. Further examples of transfer-function models appear in Chapter 9.
Next Section:
Sampling the Impulse Response
Previous Section:
More General Finite-Difference Methods




















