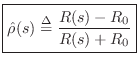DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Summary of Wave Digital Elements

From Eq.$ \,$(F.1), we have that the general reflectance of impedance $ R(s)$ with respect to the reference impedance $ R_0$ in the wave variable formulation is given by

$\displaystyle \fbox{$\displaystyle \hat{\rho}(s) \isdef \frac{R(s)-R_0}{R(s)+R_0}$} \protect$ (F.13)

In WDF construction, the free constant in the bilinear transform is taken to be $ c=1$. Thus we obtain $ \hat{\rho}_d(z) = \hat{\rho}[(1-z^{-1})/(1+z^{-1})]$. When $ R(s)$ is first order, it is possible to choose the reference impedance $ R_0$ so as to eliminate the delay-free path in the digital reflectance $ \hat{\rho}_d(z)$, and so its value depends on the actual physical element being digitized.

Next Section:
Wave Digital Mass
Previous Section:
A Physical Derivation of Wave Digital Elements