Total Energy in a Rigidly Terminated String
The total energy ![]() in a length
in a length ![]() , rigidly terminated, freely
vibrating string can be computed as
, rigidly terminated, freely
vibrating string can be computed as
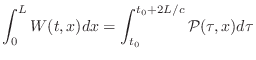 |
(C.54) | ||
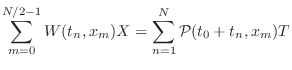 |
(C.55) |
for any
Next Section:
Plane-Wave Scattering
Previous Section:
Root-Power Waves
The total energy ![]() in a length
in a length ![]() , rigidly terminated, freely
vibrating string can be computed as
, rigidly terminated, freely
vibrating string can be computed as
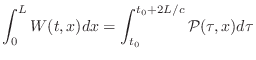 |
(C.54) | ||
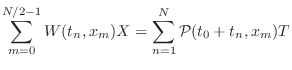 |
(C.55) |