Transfer Functions
As developed in Book II [449], a discrete-time transfer function is the z transform of the impulse response of a linear, time-invariant (LTI) system. In a physical modeling context, we must specify the input and output signals we mean for each transfer function to be associated with the LTI model. For example, if the system is a simple mass sliding on a surface, the input signal could be an external applied force, and the output could be the velocity of the mass in the direction of the applied force. In systems containing many masses and other elements, there are many possible different input and output signals. It is worth emphasizing that a system can be reduced to a set of transfer functions only in the LTI case, or when the physical system is at least nearly linear and only slowly time-varying (compared with its impulse-response duration).
As we saw in the previous section, the state-space formulation nicely
organizes all possible input and output signals in a linear system.
Specifically, for inputs, each input signal is multiplied by a ``![]() vector'' (the corresponding column of the
vector'' (the corresponding column of the ![]() matrix) and added to the
state vector; that is, each input signal may be arbitrarily scaled and
added to any state variable. Similarly, each state variable may be
arbitrarily scaled and added to each output signal via the row of the
matrix) and added to the
state vector; that is, each input signal may be arbitrarily scaled and
added to any state variable. Similarly, each state variable may be
arbitrarily scaled and added to each output signal via the row of the
![]() matrix corresponding to that output signal.
matrix corresponding to that output signal.
Using the closed-form sum of a matrix geometric series (again as
detailed in Book II), we may easily calculate the transfer function of
the state-space model of Eq.![]() (1.8) above as the z transform of the
impulse response given in Eq.
(1.8) above as the z transform of the
impulse response given in Eq.![]() (1.10) above:
(1.10) above:
Note that if there are
In the force-driven-mass example of the previous section, defining the
input signal as the driving force ![]() and the output signal as the
mass velocity
and the output signal as the
mass velocity ![]() , we have
, we have ![]() ,
,
![]() ,
, ![]() ,
and
,
and ![]() , so that the force-to-velocity transfer function is given by
, so that the force-to-velocity transfer function is given by
![\begin{eqnarray*}
H(z)
&=& D + C \left(zI - A\right)^{-1}B\\ [5pt]
&=&\begin{ar...
...{z-1}{(z-1)^2} \eqsp \zbox {\frac{T}{m}\frac{z^{-1}}{1-z^{-1}}.}
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img293.png)
Thus, the force-to-velocity transfer function is a one-pole filter
with its pole at ![]() (an integrator). The unit-sample delay in the
numerator guards against delay-free loops when this element (a mass)
is combined with other elements to build larger filter structures.
(an integrator). The unit-sample delay in the
numerator guards against delay-free loops when this element (a mass)
is combined with other elements to build larger filter structures.
Similarly, the force-to-position transfer function is a two-pole filter:
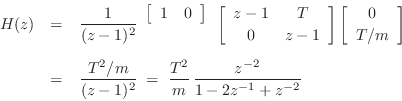
Now we have two poles on the unit circle at ![]() , and the impulse
response of this filter is a ramp, as already discovered from the
previous impulse-response calculation.
, and the impulse
response of this filter is a ramp, as already discovered from the
previous impulse-response calculation.
Once we have transfer-function coefficients, we can realize any of a large number of digital filter types, as detailed in Book II [449, Chapter 9].
Next Section:
Modal Representation
Previous Section:
Linear State Space Models




















