Free Books
   Free Books    Physical Audio Signal Processing  

Use of the Chain Rule

These traveling-wave partial-derivative relations may be derived a bit more formally by means of the chain rule from calculus, which states that, for the composition of functions $ f$ and $ g$, i.e.,

$\displaystyle y(x) = f(g(x)), $

the derivative of the composition with respect to $ x$ can be expressed according to the chain rule as

$\displaystyle y'(x) = f^\prime(g(x))g^\prime(x), $

where $ f^\prime(x)$ denotes the derivative of $ f(x)$ with respect to $ x$.

To apply the chain rule to the spatial differentiation of traveling waves, define

\begin{eqnarray*} g_r(t,x) &=& t - \frac{x}{c}\\ [10pt] g_l(t,x) &=& t + \frac{x}{c}. \end{eqnarray*}

Then the traveling-wave components can be written as $ y_r[g_r(t,x)]$ and $ y_l[g_l(t,x)]$, and their partial derivatives with respect to $ x$ become

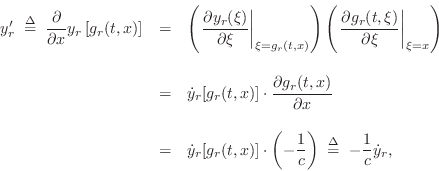
\begin{eqnarray*} y'_r\;\isdef \; \frac{\partial}{\partial x} y_r\left[g_r(t,x)\... ...t \left(-\frac{1}{c}\right) \;\isdef \; -\frac{1}{c}{\dot y}_r, \end{eqnarray*}

and similarly for $ y'_l$.

Next Section:
String Slope from Velocity Waves
Previous Section:
Traveling-Wave Partial Derivatives