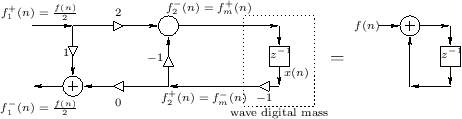
Wave Digital Filters
The idea of wave digital filters is to digitize RLC circuits (and certain more general systems) as follows:
- Determine the ODEs describing the system (PDEs also workable).
- Express all physical quantities (such as force and velocity) in
terms of traveling-wave components. The traveling wave
components are called wave variables. For example, the force
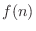 on a mass is decomposed as
on a mass is decomposed as
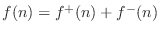 , where
, where
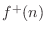 is regarded as a traveling wave propagating toward
the mass, while
is regarded as a traveling wave propagating toward
the mass, while
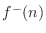 is seen as the traveling component
propagating away from the mass. A ``traveling wave'' view of
force mediation (at the speed of light) is actually much closer to
underlying physical reality than any instantaneous model.
is seen as the traveling component
propagating away from the mass. A ``traveling wave'' view of
force mediation (at the speed of light) is actually much closer to
underlying physical reality than any instantaneous model.
- Next, digitize the resulting traveling-wave system using the
bilinear transform (§7.3.2,[449, p. 386]).
The bilinear transform is equivalent in the time domain to the
trapezoidal rule for numerical integration (§7.3.2).
- Connect
 elementary units together by means of
elementary units together by means of  -port
scattering junctions. There are two basic types of scattering
junction, one for parallel, and one for series connection.
The theory of scattering junctions is introduced in the digital
waveguide context (§C.8).
-port
scattering junctions. There are two basic types of scattering
junction, one for parallel, and one for series connection.
The theory of scattering junctions is introduced in the digital
waveguide context (§C.8).
We will not make much use of WDFs in this book, preferring instead more prosaic finite-difference models for simplicity. However, we will utilize closely related concepts in the digital waveguide modeling context (Chapter 6).
Next Section:
Digital Waveguide Modeling Elements
Previous Section:
Impedance Networks