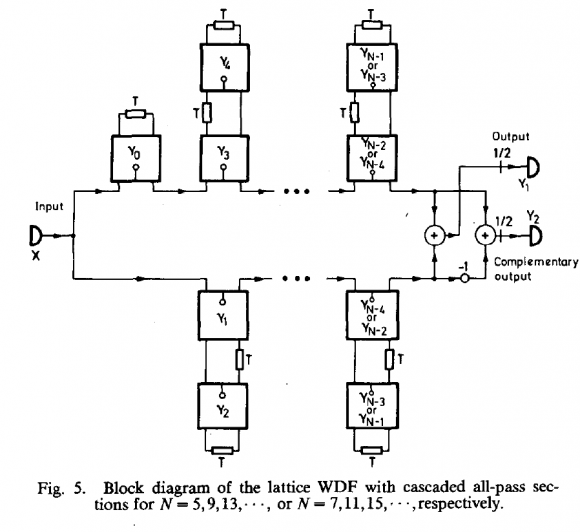
The paper  "Explicit formulas for lattice wave digital filters" by L. Gaszsi, states that LWDF are represented by two parallel branches which are realized through all-pass filters (see Fig.5). 

These filters are composed of cascades of first- and second-order symmetric two port adaptors (Fig 3 and 4). 

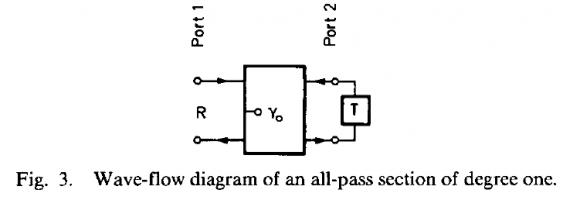
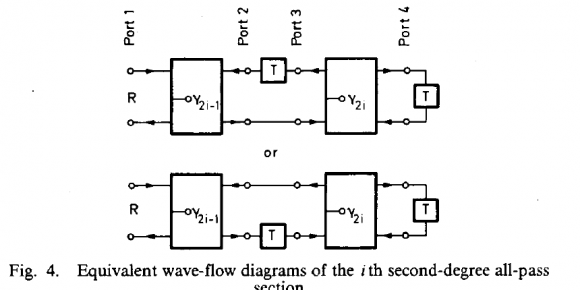
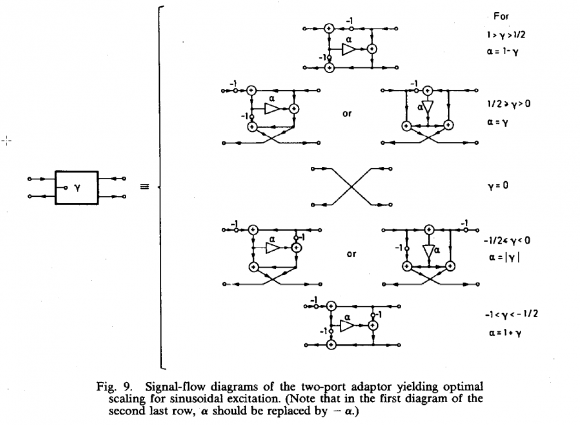
In Fig. 9 different two-port adaptors arre presented:

In a paper by L.Wanhammer ("Design of linear-phase lattice wave digital filters") I found that the transfer function for the first order section is:

$$ \frac{-\alpha_0 z +1}{ z - \alpha_0}$$.

My first question addresses specifically the first order adaptors.

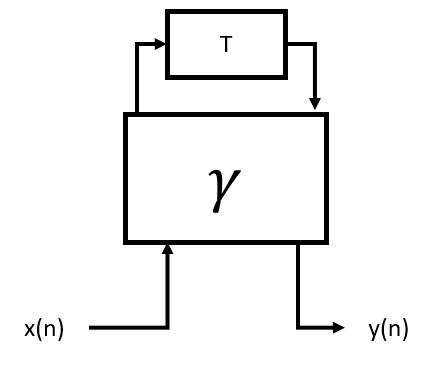
I tried to derive the differential equation from the signal flow graph (e.g. using for 1/2 > gamma >0 as in Fig.9 above ) to confirm the equation by Wanhammer.
However, I am not sure what I am doing wrong as I am failing to reduce it to x and y only.
1) Can anyone show me how to do it correctly?

My second question is regarding the definition of WDF in generall:

2)Would the use of one adaptor only as in the question above be already considered as a WDF or does it need to be derived from an analog filter which is transformed into the digital domain?

Hello Hirnprinz,

The wave digtal filter is an all-pass filter. The various signal flow graph images in figure 9 will implement them. I have a fondness for the last one in the set. I learned about this class of filters from a 1983 paper by constantinides and valenzuela and was enchanted by them. They became chapter 11 in my textbook on multirate signal processing. a PDF of a lecture I give on polyphase all-pass filters is attached. I have a collection of design routines that design the all-pass two path networks. copy tony_des_2 and tonycxx to same directory, tony_des_2 is the executable... it brings up a figure with entry points for the filter variables. I also have an M-path extension of the two-path filter with linear phase and minimum phase versions of the all-pass engines. Look at the text book for details or pass back questions to me....

fred h  

tony_des_2.m

tonycxx.m

All-Pass Filters_3.pdf

Hello fred

thanks for pointing me to your book and making your lecture available (and the matlab files). I will go through the slides this weekend and try to get your text book as I am really interested in this subject.

hello Hirnprinz,

me again (fred h) from my read -e file describing various all pass script files

two are attached

two_path_compare.m

two_path_demo.m

1. tony_des_2

Graphical user interface (GUI) driven script file presents coefficients of two-path recursive all-pass filters. The two path filter options include half-band filters, an option to tune the half-band filter to an arbitrary bandwidth, an option to tune the filter to an arbitrary center frequency, and an option to zero pack the impulse response for iterated filter designs. Two figures are formed by tony_des_2, the frequency response and the pole-zero diagram of the designed filter. The script file tony_des_2 a second script file tonycxx.

1. two_path_demo

Script file to illustrate the phase relationship between the two paths of a two-path, recursive all pass filter. The file generates 5 figures showing the phase response of the two paths and the magnitude response obtained by adding the outputs from the two paths. The particular filters are a linear phase, recursive half band low pass filter, a non uniform phase, recursive half band low pass filter, a non uniform phase, recursive 10% bandwidth low pass filter, a non uniform phase, recursive 2.5% bandwidth low pass filter, and a non uniform phase, recursive 15% bandwidth band pass filter.

Hello fred,

once again thank you for pointing me to your text book. The chapter you mentioned (recursive polyphase filter) adressed my question and helped to give me more insights into this subject.

I have some question:

1) In the subsections regarding "two-path half band filters: nonuniform phase" and also for the "linear phase" I am not sure how the coefficients are derived? You are speaking about "comparing it to the appropriate Pascal triangle". How exactly does this work? Where can I read more about this subject? Also how does someone estimate the appropriate number of sections for each path?

2)For a low pass filter with an arbitrary band width, I would have the same questions. How do I relate the filter specifications (stop/pass band edges,etc..) to the polynomial coeffiecients and the number of sections?

3)And the same for the M-path filters: how do you estimate the sections per path and the coefficients? Could you share your extension for that?

hello hirnprinz,

The design of the 2-path minimum phase filter came from discussions with Tony Constantinides. You have that copy in tonydes_2 (tony for anthony). The design of the M-path filter came from two papers by Markku Renfors 1987 paper "Recursive N-th Band Digital filters". I along with 2 of my grad students reproduced his work. Years later I asked Markku if I could compare my version of the two script files (minimum phase and linear phase) with his version. He let me know that he no longer had his original code. Thus it seems I am the keeper of the code that forms the M-Path filters. The code solves a set of non linear equation in ATAN space. Markku linearized each iteration and iteritivly converged to the correct solution. Very clever. 

I distribute my versions of the code: nonlineardesign_2 and lineardesign_2. I wold need an email address. Each contains numerous functions called by a main program. I recall making a prsentation in Autralia on the linear phase version and left a copy with the grad students with a request not to distribute it till I could publish a paper on it. When I returned home I found that they had listed it on their web page with a thank you to me for sharing it with them. 

Hello fred,

I found the papers by Renfors, looking forward to get into this subject. Once again thanks for pointing me to them.

Regarding your M-path filter function I wrote you a message with my email address. Thank you for sharing your code.

Hello hirnprinz

I just finishd a search of my email and have not found the note from you. 

fjharris@eng.ucsd.edu

fred