Hello,

I've been working on a Master's Thesis regarding Convolution Reverb, and had a question I was hoping someone could answer.

When it comes to using multiple impulse responses to convolve an #Audio signal, how easy is it to exactly derive an impulse response?

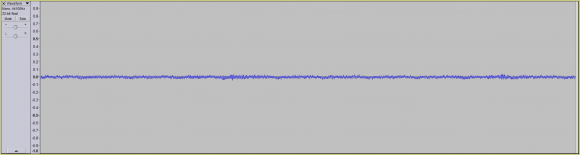
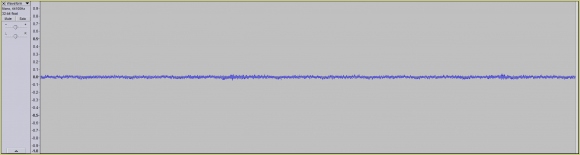
For example, let's say I provided you the following dry signal:

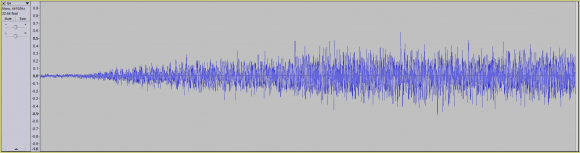
Let's say I then convolved the signal using two different IR's (IR A and IR B), and then provided you the convolved signal:

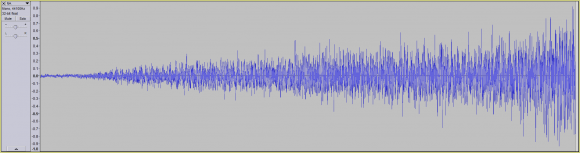
Let's also say I then convolved the signal once more (using IR A and a new IR, IR C), and then provided you the newly convolved signal:

Question: Is it a trivial to derive IR A?

Thank you,
Nelson

I'd say "no" in the context of what *I* think is trivial.  :-)

Hi.  What does it mean to "convolve a signal with two impulse responses"? Is the result of such a process one output sequence or two separate output sequences?

Hello Rick,

My apologies for my unclear statement.

Convolving a signal with two impulse responses is merely taking a dry signal:

...and convolving it with one impulse response (resulting in the following waveform):

...followed by convoling the resultant waveform with another impulse response (resulting in the following waveform):

So the question becomes, if you only had access to:

a. The dry signal

b. The first convolved signal, which equates to the dry signal convolved with impulse response "A", followed by the convolution of impulse response "B".

c. The second convolved signal, which equates to the signal from "b", convolved with impulse response "A" (for a second time), followed by the convolution of impulse response "C".

Thank you,
Nelson

???? I know I responded to this but I don't see it here.

Hello Fred,

It's unfortunate that your response wasn't recorded.

That being said, a simple "yes" or "no" would suffice (just to save you the trouble of having to rewrite what you previously wrote).

Thank you,
Nelson

With regard to "trivial," I would say that anyone with a basic competency in signal processing should know that a convolution in the time domain is equivalent to a multiplication in the frequency domain.  To put it another way:

y(t) = x(t)*h(t)  (convolution)

Y(w) = X(w)H(w) (multiplication)

Where Y is the output, h is the impulse and x is the input, and a capitalization indicates the Fourier transform of the signal.

This identity is also true for discrete time, such as your digital audio waveforms.  So, given your problem statement, how would you relate your signals mathematically?  You should then have a system of equations.  If you can use the system of equations to show that the desired signal can be calculated (or not) you're done.  It's really not harder than doing basic algebra.

Nelson,

I believe one issue you would have when trying to deduce an impulse response by comparing the convolved and unconvolved signal pairs is uniqueness: there may be multiple IRs that could give rise to the same signal. (I am thinking of this in the context of fitting multiple exponentials to a decay curve). But if you have access to a good set of signal pairs and you have a general idea of what the IR should be like that might improve your chances of getting a good fit. I would try with some simulated data + noise and known/made up IRs. Convolve them, then deconvolve the result with the input signal (or the input IR) and see how far off the resulting IR (or input signal) is. You may find the accuracy will vary depending on the IR and signal.  

I am not an expert, so I hope you get some more opinions :)