Hello,

In Matlab, I am currently generating a chirp with a sampling frequency sampling of 200e6 Hz, starting at t=0s to 1ms, and f0=1Hz to f=2e6 Hz at the end of the signal.

It looks something like that :

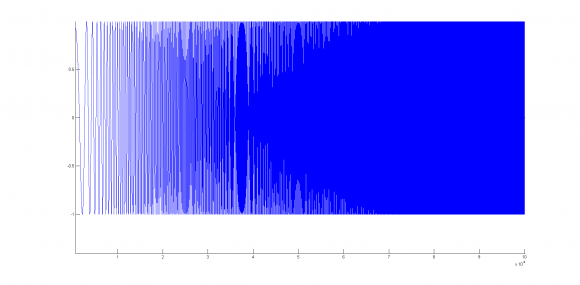
However I am looking to transform this signal into a complex signal in order to put it through a IQ modulator.

I am using the hilbert transform to do that. So in matlab : hilbert(MyChirp);

The Hilbert Transform should shift my signal of 90° and transform in into a complex signal right ?

But when I plot the imaginary part of the complex signal, here is what I got :

The amplitude has changed. I though the Hilbert Transform kept the same amplitude ?

When I zoom :

So I though, what if I divide my imaginary part by abs(MyComplexChirp). Don't ask me why I did that...

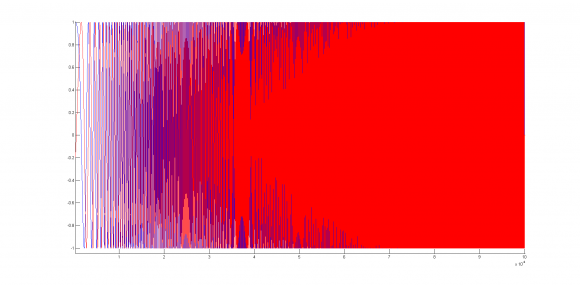
In red is the imaginary part divided by abs(MyComplexChirp). It's still 90° shifted, however, when I close up when the frequency gets higher :

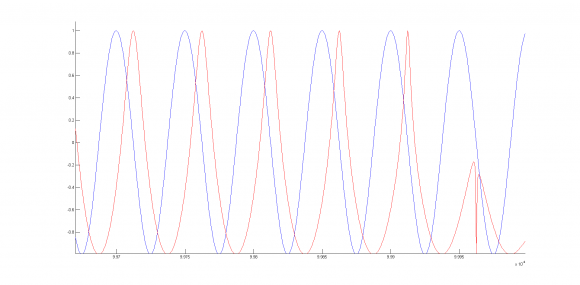
Now we can see that it is not what I want...

Can someone help me and explain me why isn't the amplitude the same as the real signal after the Hilbert Transform ?

Thank you

BR

In order to create a signal that is shifted by 90 degrees, the Hilbert filter is an interpolator. This virtually requires some sort of low pass filtering.  That seems to be why you are getting some funny activity near the highest frequencies.

Are you really expecting to obtain a valid signal all the way to exactly Fs/2?

If that is what you really want, then why not create the sweep as a complex vector right from the start.

complex(MyChirp_using_cosine, MyChirp_using_sine)

David

Thank you so much for your help, I haven't think about the complex function and generating 2 chirp using cosine and sine.

Thank you, it works fine !