As a test engineers and application engineers for Mixed Signal Testing it is important to create the best environment for the device to succeed.  By "environment" I mean frequency spectrum. 

Coherent Sampling (#CoherentSampling) simply describes a rational relationship between the input frequency and the sampling frequency. Typically, when discussing coherent sampling in device testing, additional constraints are enforced in the relationship to ensure the best possible frequency spectrum. 

When these constraints are met, spectral leakage will be minimized. Spectral Leakage is simply the power of  fundamental tones and their respective harmonics to be spread over multiple bins. Hence the naming spectral leakage: the power of signal is "leaked" into other bins of the spectrum. 

I intend to keep this post extremely short and not dive into details. I plan on providing more posts later that dive into the mathematics and how they are realized on ATE. Specifically, the Advantest v93K. (I wanted to first see if I could even make a post!).

Below is slide from a recent presentation I gave on Coherent Sampling. This particular slide aims to illustrate where the coherent sampling equation comes from. Please, give feedback if you have some to give. I am here to LEARN and CONTRIBUTE. 

Thanks,
MS

Very nice & concise! I have added the results of two simulations of an 14-bit ADC, showing the effect of choosing M/N non-prime vs. prime:

Choosing M/N non-prime repeats the signal quantization periodically and fewer quantization steps are measured. The quantization repeats periodically and creates a line spectrum that can obscure real frequency lines (e.g. the red lines in the images below, created by non-linearities of the ADC).

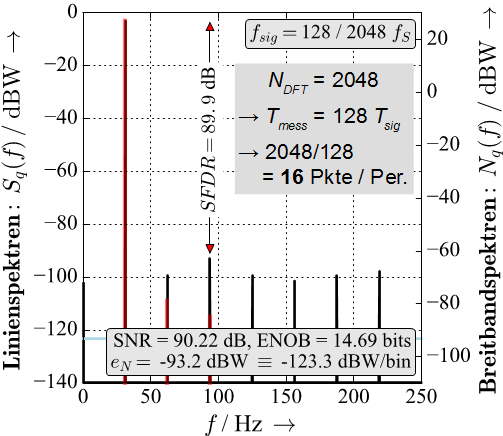
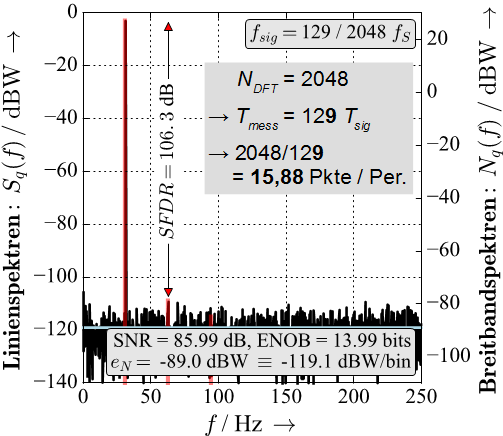
@chipmuenk nice to see you on here!

I do that quite often with control systems when I have a SAR ADC -- sample the ADC as fast as it'll go, then use the sum of the resulting samples at the control loop's sample rate.

Hi Tim,

Can you elaborate on this?what is the input to the ADC in this case? What is the goal here? Seems interesting but I can't quite figure out the system. 

The input to the ADC is various.

The motivation is that most successive-approximation ADCs have a significant amount of noise.  The pertinent features are that it generally has a deviation that's well over 1LSB, and it is generally broadband compared to the ADC's highest sampling rate, and is thus essentially white no matter how rapidly you sample.

This means that if you can sample the ADC significantly faster than your control loop's sampling rate, and if you can sum up a vector of those samples at each iteration of your control loop at low cost, then you can get samples that are much lower noise than what comes straight out of the ADC, and which can actually have a higher precision (but not accuracy) than the bit-count of the ADC.

As an added bonus, the frequency response of the resulting filter has a sync response, with a fairly uniform gain at low frequencies, but with nulls at each harmonic of the sampling frequency.  If you happen to have a system that has external noise at high frequencies that might alias down to within the control loop bandwidth, doing this will attenuate that noise significantly.

A detriment, which I almost never find to be significant, is that the filter adds an average delay of a half-sample of the control loop sampling rate.  This is really only an issue if your loop is clinging to meeting goals by its fingernails, and if there's some reason that you can't increase the sampling rate.

Why M and N should be mutually prime? I can see some explanation in chipmuenk post but I still can't get it.

The way I like to conceptualize it is that one does not want an whole-number amount of samples over each repeating cycle - unless you are sampling one cycle.  

For example, if one chooses M = 3 and N = 24 (normally we would set N to a power of 2 and but for the sake of the example, we don't care), then this would result in 8 samples per cycle and, like you said, you will have redundant codes which yield periodic quantization errors.

In this case, one possibility is to pick M = 5 and slow the sampling rate down accordingly (assuming they are set on N = 24). This will allow the user to hit more codes of the full-scale range.

This is not detailed but it might help conceptually.