The paper is behind the oddest sort of paywall -- so maybe I'll get a copy, maybe not.

In the mean time, I don't particularly believe in putting in a lot of effort to map a controller from the s-domain into the z-domain.  Rather, it's not terribly difficult to get an exact model of the plant's behavior as seen by the controller from the plant's s-domain model and the sampling rate.  With this model in hand, you can then go and design a controller from the ground up in the z domain.

Paper can be found from here (soar.wichita.edu -link).

In non-answer to your original question, I don't know of any implementations out there.  

Frankly, I don't think this is going to take the world by storm, because I think that most of the controls community agrees with my statement about just designing in the z domain.  This method is akin to a buggy whip with a custom-designed carbon fiber shaft -- it may be optimal for its kind, but its kind is obsolete.  So I doubt that many people have jumped on it.

I think your best bet would be to see if you can track down the author, or perhaps the author's thesis advisor, and ask.  If it's an on-going research topic then the thesis advisor should have something.  If the author still uses it, then he should have something.

Thanks!

So far I've got info that any algorithm that relies on cepstral methods does not work if the analog transfer function is zero at any point.

Actually, instead of controls my aim is to try these methods for to improve biquad LPF 'output' at low sampling rates. Dunno if these methods can be even used for that task and since my knowledge level regarding DSP and involved math is quite low (i.e. that paper tells me nothing), finding some source code (C/C++) would help me to start do some experiments.

I'm not sure why the author feels he has to do cepstral processing, unless it's because he's trying for IIR filters.

There are other ways of making an IIR filter fit closely to a desired amplitude response.  At the risk of going beyond your current understanding of this stuff, I think that what you want to do is:

• Define the amplitude response you want when all is said and done
• Divide out the effects of any anti-aliasing filters, ADC response (particularly if it's sigma-delta), reconstruction filters, and the natural zero-order hold action of the DAC (unless it's sigma-delta, in case it won't be a zero-order hold, but it will be something)
• What's left is the response you want your IIR filter to have.  Do a best-fit to that by the method of your choice
• Put it all together and try it out

I ran the Matlab listings from paper (needed some modifications) but got only the MIM plot 'correctly' (not exact figures compared to paper):

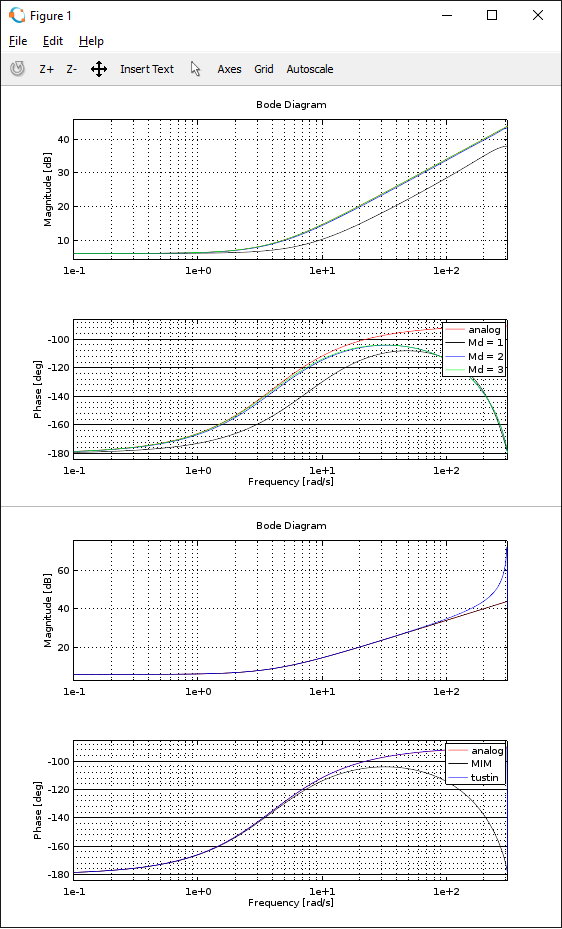
In original Matlab script there are two sets of coefficients given ... for 'plant' and 'analog' filter. How these should be set for LPF filter? Also, what should be done to get the frequency changed from rad/s to Hz units?

Magnitude responses looks promising.

2nd order MIM LPF results looks great for selected cutoff frequency (fs = 44.1kHz) as seen in plot (frequency range upto 23873Hz):

Coefficients for 2nd order LP filter showen in plot:

a [ 0.437417389844334 0.1220119196463959 -0.04071587087954469 ]
b [ 1 -0.6951293456643256 0.2138427842755107 ]

I have not checked the magnitude error agains analog model.

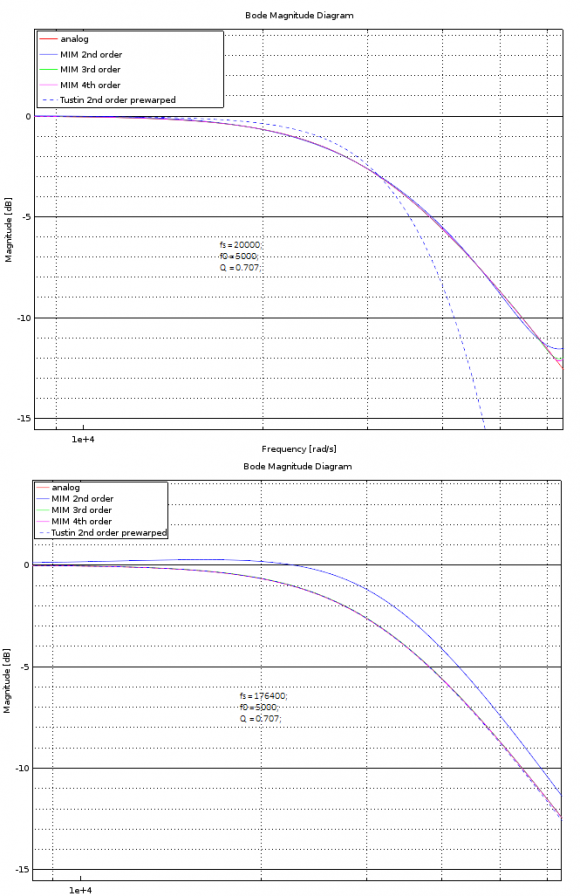
At 44.1kHz sampling when fc is set to 20Hz, situation looks this bad:

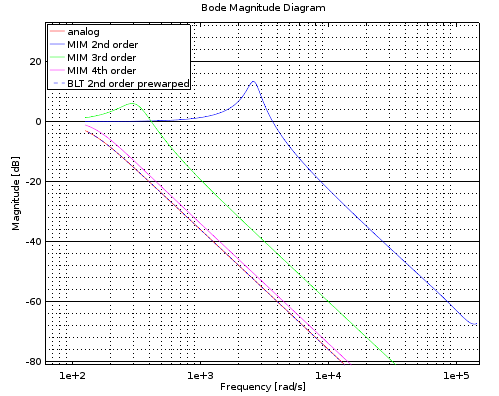
MIM/PIM paper mentions this as an issue.

So, it looks like MIM can be used for to improve 2nd order LPF magnitude response especially when using low fs and high enough fc. Magnitude response issues can be rounded by using higher order filters. Fortunately MIM method works correctly for my purposes.