I want to compare different implementations of CIC decimation filters and came across the following question here in the forum: Polyphase CIC. In one of the answers Rick posted a link to a thesis (A POWER EFFICIENT POLYPHASE SHARPENED CIC DECIMATION FILTER FOR SIGMA-DELTA ADCs). 

Now I want to implement a sharpened CIC (SCIC) filter myself and play with the parameters to get a better understanding of its behaviour. I am focusing on the following equation (2.16 in the thesis):

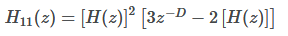
Where D is the group delay of the filter H(z) (in this case a first order CIC filter with the decimation factor N).

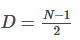
The magnitude response of such a SCIC with order K=1 is given by:

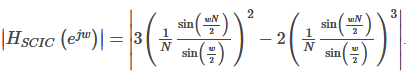
So far so good.

Now, I am attempting to implement equation 2.16 directly. Additionally I want to compare the magnitude response of my implementation with 2.18. However, in the case N=16, the group delay D is 7.5 and I am not sure how to implement this. Here is my approach so far (in Matlab):

<code>Fs=16*150;</code><code>
%length of H filter
N=16;
% impulse response of H (here a cic first order)
h=ones(16,1)/16;

% H^2
cic_2nd= conv(h,h);
%Group Delay of H
D=ceil((N-1)/2);
%Delay line with gain
b=zeros(N,1);
b(D)=3;

% temporary impulse response
h_tmp=b-2*h;

% final impulse responses</code><code>
hfinal=conv(cic_2nd,h_tmp);

% final frequency responses
[H_fin,F_fin]=freqz(hfinal,1,Fs,Fs);

%Theoratical Response (2.18)
K=1;
N=16;
omega=linspace(0,1,Fs)*pi;
G = (sin(omega*N/2)./sin(omega/2))/N;
H_tr = abs(3*G.^(2*K) - 2*G.^(3*K));</code>

As you can see I have to round D by taking the ceil of (N−1)/2. Comparing now the theoretical magnitude response with my approach I can see a deviation in the passband (0 to 30Hz):

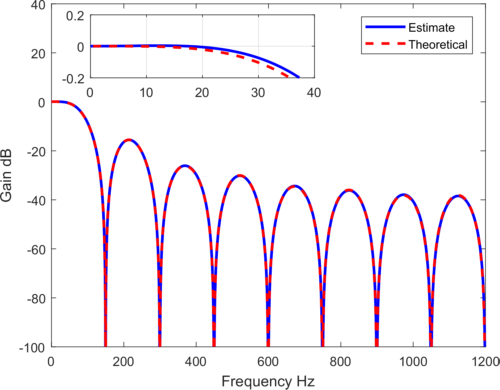
So my question is, how do I have to adapt my code to implement a SCIC wiht order K=1 and the theoretical D which has to be a non-integer (D=7.5) in the given situation? 

Hi hirnprinz. My congratulations to you on your very clearly written question. 

The delay 'D' must be an integer when using the standard "Filter Sharpening" scheme shown below (copied from Chapter 13 of my "Understanding DSP" book):

Because the above 'Delay' element must be an integer number of unit delays, to keep the two sequences applied to the adder synchronized in time the group delay of the h(k) filter must be an integer. This means your MATLAB value 'N' must be an odd number.

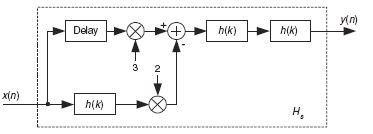
Hi Rick, thanks for your answers. 

I already assumed that the 'Delay' limits the choice of the filter (the length of the filter). However, I was not sure about it as the author of the thesis did not make any statements about that. But reading your answer makes it obvious.

Hi hirnprinz. I posted my original reply and then a minute or two later realized that the second part of my reply was incorrect. So I deleted the second part of my reply. But you saw my original reply BEFORE I made my deletion. Sorry for the confusion!!

I think your MATLAB code is computing what you intended and contains no errors. But keep in mind, to model a correctly-sharpened 'moving average' filter you need set N to an odd number.

Once again, thank you very much. I will adapt my code regarding the parameter 'N' and hopefully extend it succesfully to a polyphase version.