I am working on writing my own SDR software.  I have receiver hardware that delivers IQ data decimated down about ten khz coming in in packets of 480 complex samples (float precision) at about 22 packets per second.  The resolution at that level of decimation is over 24 bits.

My goal is to implement all the functions of a receiver with DSP.   My strategy will be to FFT the incoming packets, Apply high performance filters and other kinds of processing in the frequency domain, and then IFFT back to time domain with overlap-add, different types of demodulation, and obtain the audio.

I am at the beginning stage of FFTing one packet of data, simulated with sine and cosine.   I have implemented Complex FFT and a number of different windows.  The results all look like the textbook results of width and side lobes with Hamming, Hanning, Nutall, BH92, and so forth.   

I am assuming that each packet of samples will have to be windowed on both I and Q channels.  And I understand why windowing needs to be applied to the time domain packet before FFT.   What I don't understand is how this does not create dramatic artifacts in the reconstituted signal at the end of the overlap and add process.   It would seem like rather than a continuous stream of sampled audio, it would appear like beads on a string, if you can imagine the packets reassembled at the end from heavily windowed packets going in to the process.

Also, I don't have a good feeling for how to choose the window.  Given that this is just conditioning the time domain packets for FFT, do I need to worry more about band broadening or sidelobe suppression as a priority?    Do I need windowing at this part of the process at all?

My sources so far are books by Rick Lyons and Steven W, Smith.

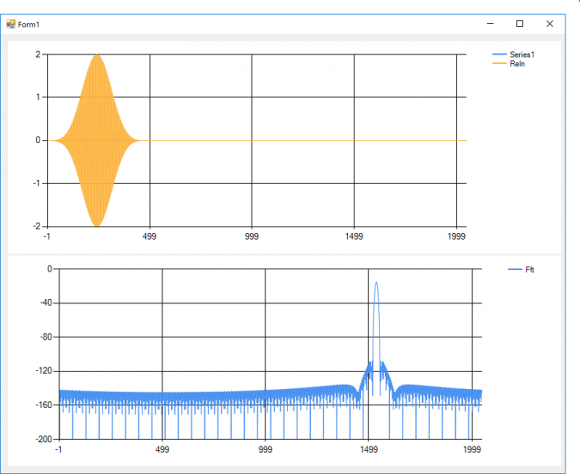
An Example:
480 samples zero-filled to 2048 samples, 10 Khz sample rate,  2500 Hz signal, 0 degree phase in real, 90 degrees phase in imaginary channel.  Four term Blackman-Harris window.

Thanks in advance for any advice. 

This raises the issue of continuous stream processing Vs packet based processing.

If your system is continuous stream then I would not go for fft but do filtering directly in time domain. I wouldn't do fft/ifft unless there is good reason. For example when data is indeed meant to be processed as packets such as lte symbols. 

No, it is a stream of I/Q data being sent in blocks.  There is no protocol in the actual data itself.  I think that ordinarily you would be right. It would be a lot easier, and I have more familiarity with time domain IIR and FIR filters.

But the amateur bands are crowded and the dynamic range of signals side by side is really big.  During a contest or a pileup on a station from some remote island the signals are packed in like sardines.  The filtering requirements are such that doing fft/ifft is pretty much the unanimous choice of all the high end DSP software products.   I am talking about "brickwall" filters with a thousand or more points and the ability to move the filter cutoffs at anytime depending on needs.   Whereas, the common wisdom is that the threshold for using FFT/IFFT multiplication filtering instead of convolution is about 60 - 80 points.  

Also, all the cool kids now have waterfall displays.

On the other hand, I am a novice at this, so I appreciate the advice. I will keep an open mind about this.

This is what I am trying to accomplish, which is FFT Convolution where bandpass filters on the order of a thousand taps or so are applied in the frequency domain to blocks of data in a very long data stream.

All the examples I can find show no window kernels applied to the signal before the FFT convolution happens.  Is this just for simplicity in the explanation or is it because it is just not necessary?   Does the FFT convolution take care of the leakage problem intrinsically?  Thanks in advance for any advice.

http://www.dspguide.com/ch18/3.htm

The use of fft/ifft for equivalent correlation or convolution as that of time domain is only equivalent (mathematically sample by sample) if you use the proper fft resolution, avoid any windowing but insert zeros in the right sections then multiply,followed by ifft.

If you do windowing then you wouldn't get that equivalence but you might want to do windowing for other reasons and then accept the penalty.

Thanks very much for that reply, kaz.  That answers my original question. 

Also, the books and other examples that I have are quite good on fft resolution, zero filling in the right sections for overlap-add and so forth.  I will go off and see what I can do.  Thanks again.

Hello wa1x.

If you're using FFTs to implement high-performance digital filtering, in a process called "fast convolution", then there is no need to window the time-domain samples prior to performing FFTs. Windowing of time-domain samples, to reduce spectral leakage, is only used in some (but not all) spectrum analysis applications.

You should avoid windowing your signal samples in a digital filtering application. That's because windowing would induce unwanted amplitude modulation (AM) distortion at the beginning and end of your filtered signal packets.

wa1x, if you have a copy of my "Understanding DSP" textbook you may want to have a look at the following web page:

https://www.dsprelated.com/showarticle/1094.php

Good Luck,

[-Rick Lyons-]

Excellent. Thanks again to both of you.  I do have your book and it has been a great help.  I think I got off on the windowing tangent because I was reading all the introductory sections on FFT of finite length data.   

And yes, my main concern was that if I were to window the segments of data, it would be like AM modulating the signal.

- WA1X