Three-Term Blackman-Harris Window
The classic Blackman window of the previous section is a three-term
window in the Blackman-Harris family (![]() ), in which one degree of
freedom is used to minimize side-lobe level, and the other is used to
maximize roll-off rate. Harris [101, p. 64] defines the
three-term
Blackman-Harris window as the one which uses both degrees of
freedom to minimize side-lobe level. An improved design is given in
Nuttall [196, p. 89], and its properties are as follows:
), in which one degree of
freedom is used to minimize side-lobe level, and the other is used to
maximize roll-off rate. Harris [101, p. 64] defines the
three-term
Blackman-Harris window as the one which uses both degrees of
freedom to minimize side-lobe level. An improved design is given in
Nuttall [196, p. 89], and its properties are as follows:
-
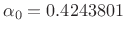
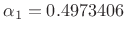 , and
, and
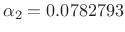 .
.
- Side-lobe level
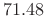 dB
dB
- Side lobes roll off
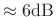 per octave in the absence of aliasing
(like rectangular and Hamming)
per octave in the absence of aliasing
(like rectangular and Hamming)
- All degrees of freedom (scaling aside) are used to minimize side lobes (like Hamming)
Figure 3.14 plots the three-term Blackman-Harris Window and its transform. Figure 3.15 shows the same display for a much longer window of the same type, to illustrate its similarity to the rectangular window (and Hamming window) at high frequencies.
Next Section:
Frequency-Domain Implementation of the Blackman-Harris Family
Previous Section:
Matlab for the Classic Blackman Window








![\includegraphics[width=\twidth]{eps/blackmanHarris3}](http://www.dsprelated.com/josimages_new/sasp2/img420.png)
![\includegraphics[width=\twidth]{eps/blackmanHarris3Long}](http://www.dsprelated.com/josimages_new/sasp2/img421.png)











