An Interesting Fourier Transform - 1/f Noise

Posted by Steve Smith on Nov 23 2007 under Academia / Research   

Power law functions are common in science and engineering. A surprising property is that the Fourier transform of a power law is also a power law. But this is only the start- there are many interesting features that soon become apparent. This may even be the key to solving an 80-year mystery in physics.

 

It starts with the following Fourier transform:

 

 

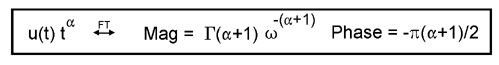
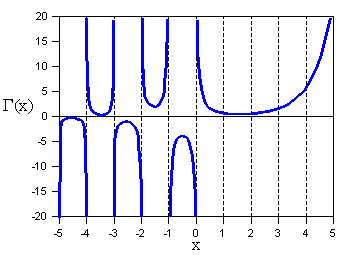
The general form is t^α ↔ ω^-(α+1), where α is a constant. For example, t² ↔ ω^–3 and t ^-0.75 ↔ ω^–0.25. Unfortunately, there are additional terms that distort this simple relation. First, the left side contains the term, u(t), the unit step function. This is defined as u(t) = 0 for t < 0, and u(t) = 1 for t ≥ 0. In other words, this makes the time domain a one-sided power law. Second, the power law in the frequency domain only pertains to the magnitude; there is a phase term that doesn't resemble a power law at all. Third, there is a scaling factor in the frequency domain, Γ(α +1). This is the Gamma function, which is essentially a continuous version of factorials. A graph of the Gamma function is shown below. Don't worry too much about this strange function. Think of it simply as a constant that scales the amplitude of the frequency domain, depending on the value of α.

 

 

The table below shows nine cases of this Fourier transform, with alpha running from -2.0 to 2.0, and rough sketches of the curves. The frequency domain also shows a rough sketch of the magnitude graphed on a log-log plot, which turns out to be is a straight line with a slope of -(α+1). Take a few minutes to examine this figure, especially noting the symmetry between the time and frequency domains.

 

 

One of these cases should be familiar to you, where α=0. This is the Fourier transform of the unit step function, with a magnitude of 1/ω, and a phase of -π/2. As you probably recall, this describes the impulse and frequency response of the perfect integrator. Now consider the case of an integrator followed by another integrator. The impulse response of this two stage combination is the unit step response convolved with itself. In the frequency domain the magnitude becomes 1/ω × 1/ω, and the phase becomes 2 × (-π/2). This two-integrator cascade is shown on the graph for α=1, where the impulse response is a linearly increasing line, and the frequency spectrum is 1/ω² , with φ = -π. Likewise, α=2 represents a cascade of three integrators, and so on. It is interesting that these Fourier transforms are so well behaved, in spite of both domains containing nasty features (such as: t² as t → ∞ , and ω^-3 as ω → 0 ).

 

Here is something even more interesting. As you approach α = -1, the time domain approaches a shape of t^-1, and the frequency domain approaches a flat magnitude with a zero phase. However, a flat magnitude and zero phase corresponds to a delta function, δ(t), in the time domain. That is, in the limit as α → -1, u(t)t^-α = δ(t). This is because the sharp point of t^-α grows rapidly as α → -1, dominating the entire function. But what happens exactly at α = -1? How could the sharp point ever completely negate the seemingly finite width of t^-1? The mathematics tells you not to ask this question. Recall that the frequency domain has a scaling factor of Γ(α+1). For α = -1, the gamma function is undefined.

 

Now we come to a feature that I find absolutely fascinating. In general, we have seen that a power law in one domain corresponds to a power law in the other domain. Further, there is an inverse relationship; if the time domain decays faster, then the frequency domain decays slower, and vice-versa. This means that there must be a certain decay rate that is unique, where both domains are equal. This occurs for α = -0.5, where the time domain is t^-0.5 and the frequency domain is ω^-0.5. Interesting, but what does this mean?

 

Now look at the figure below, a graph of the measured noise that originates within a common electronic amplifier. The flat section above 100 Hz is called white noise , and is well understood. However, the sloping portion below 100 Hz is not well understood at all. This is 1/f noise, a mystery that has resisted explanation for over 80 years. 1/f noise has been observed in the strangest places- electronics, traffic density on freeways, the loudness of classical music, DNA coding, and many others.

 

 

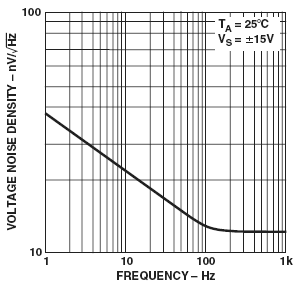
Many of the properties of noise are directly related to the amount of power in a signal, that is, to the square of the amplitude. Accordingly, most of those working with noise think in terms of power spectra, not amplitude spectra. 1/f noise gets its name because its power spectrum has a shape that is close to 1/f. However, if we look at the amplitude spectrum for 1/f noise it has a shape of 1/f^1/2. As can be seen above, on a log-log plot of amplitude, 1/f noise has a slope of -0.5. Now you can see where I’m going.

 

At least in a limited sense, 1/f noise is its own Fourier transform, with ω^-1/2 in the frequency domain, and t^-1/2 in the time domain. For instance, a single pulse given by u(t) t^-1/2 has a 1/f power spectrum. Likewise, a randomly occurring sequence of such pulses has a 1/f power spectrum, at least over a wide range frequencies. Further, 1/f noise can be created by passing white noise through a filter with an impulse response of u(t) t^-1/2. Unfortunately, none of these scenarios seems to have a physical interpretation that explains the widespread observation of 1/f noise. It’s clear that something is still missing.

 

There is also another issue: u(t) t^-1/2 is the transform pair of Mag = ω^-1/2 , φ = -π/4. However, no one knows what the phase of 1/f noise is, or even if it has a defined phase. If the phase happens to be different from φ = -π/4, then the corresponding time domain signal will also be different. That is, it may be that the characteristic time domain waveform of 1/f noise is simply not t^-1/2.

 

Nevertheless, the idea that 1/f noise is its own Fourier transform is very compelling. Consider the Gaussian curve, the most important waveform associated with random events. The Central Limit Theorem tells us why the Gaussian is so commonly observed. However, it is also true that the Fourier transform of a Gaussian is a Gaussian. This seems more than coincidence– I think it is a critical clue in solving the mystery of 1/f noise.

 

Comments are certainly welcome! I especially appreciate suggestions for new directions in research and (god forbid) errors in math.

 

Steve Smith email http://www.dspguide.com/

11/24/2007

Rate this article:
posted by Steve Smith
Steve Smith specializes in developing novel imaging systems for medical, security, and industrial applications. His interests include: digital signal processing, analog electronics, x-ray physics and sensory systems. Dr. Smith is the author of "The Scientist and Engineer's Guide to Digital Signal Processing," freely distributed over the internet in electronic form. For the last ten years he has been the president and technical director of Spectrum San Diego, Inc., a research and development group specializing in imaging and instrumentation systems.

Next post by Steve Smith: Waveforms that are their own Fourier Transform
all articles by Steve Smith

Would you like to be notified by email when Steve Smith publishes a new blog?

  

Dear Steve,

Thank you for a very interesting discussion on 1/f noise.

Time series data in the real world cover a limited time span. So a time series signal that looks like a straight line with a unit slope, when truncated, becomes a sawtooth. The amplitude of the frequency spectra of a sawtooth is 1/ω, and not the 1/ω2 for that of a linearly increasing line. I guess my point was that real life time data which had been used to demonstrate 1/f noise so far were always truncated in time. Would that consideration present any problem for your consideration of the Fourier transform of 1/f noise?

Please advise.

Woo, a student new to fft

Dear Dr. Smith,
I am a working on a paper which deals with fractional Fourier transform. Can you please provide me some material about FrFT, specially I am interested in knowing the physical/geometrical significance of FrFT, something which can explain me how FrFT of an image looks like and Inverse FrFT will look like?
Sincerely -
Rajendra Uppal

Hi Rajendra,
I've never worked with FrFT, so I don't think I can give you much help. It sound interesting-- if you have a chance I'd like to see some information on it.
Thanks,
Steve
Steve.Smith1@SpectrumSDI.com

I a generated a signal using fourier series and measured it at three different sensors by simulation of a model. I now want to reconstruct back my original signal. I carried out an fft on the three signals from the sensors and know if I can extract their amplitudes and frequencies, I can use that to get back my original signal using the fourier series. My problem now is how to extract this frequencies and also, if I should analyze all the signals from three sensors or one will be ok.
Thank you.
Ayodei

Hi Ayodei,
Fee free to contact me directly at Steve.Smith AT SpectrumSDI.com
Regards,
Steve

i'm not very strong in math, so here's my simplistic take on 1/f noise: it's already well-known that lower frequencies travel and permeate better than higher frequencies. take sound, light, or whatever. for example that's why elephants can communicate at sub-audial (for humans) frequencies over ~100 miles. so my theory is that if you have a system whose different parts, and/or even the integrated whole are generating waves at varying frequencies, the lower the frequency the better it'll permeate throughout the system, and hence at any point in the system all those lower frequencies generated anywhere within it will add up, and the higher ones won't. might this principle lead to a 1/f spectral envelope?

Dear all,

I have a doubt though it is not linked to the current discussion.

How do we calculate the snr of a signal only from its sampled observations and when the noise variance is not known a priori.

Assume
y[n] = x[n] + noise where x[n] is the original exponential signal and y[n] is the noise corrupted signal.
Now is there a way to estimate snr only from observations y[n]. Is there a way to measure noise variance and power of signal x[n] just from y[n].

Not sure if this helps the thought process but, maybe it is good to consider photons. A photon is its own antiparticle. Of course, once you get onto that road, you would have to think four dimensionally! :)