Pentagon Construction Using Complex Numbers

• Basics
• Tips and Tricks
• Tutorials

Introduction

This is an article to hopefully give a better understanding of the Discrete Fourier Transform (DFT) by showcasing a special case of the Roots of Unity, which underly the DFT. Admittedly, five bin DFTs aren't used too often, so in actuality you can consider this article another exercise of using complex numbers in context. The complex plane and the corresponding Cartesian plane are both utilized.

The Fifth Roots of Unity

A Fifth Root of Unity is a complex number when raised to the fifth power gives a value of one. Any complex number $z$ can be represented by the form $a + i \; b $ where $a$ and $b$ are real numbers. Finding the roots means solving this equation: $$ \begin{aligned} 1 + i\; 0 &= z^5 \\ &= \left( a + i \; b \right) ^5 \\ &= a^5 + i \; 5 \; a^4 b - 10 \; a^3 b^2 - i \; 10 \; a^2 b^3 + 5 \; a b^4 + i \; b^5 \\ &= \left( a^5 - 10 \; a^3 b^2 + 5 \; a b^4 \right) + i \; \left( 5 \; a^4 b - 10 \; a^2 b^3 + b^5 \right) \\ \end{aligned} \tag {1} $$

Separated Parts

In order for two complex numbers to be equal, their real parts have to be equal and their imaginary parts have to be equal. By matching equal parts, the last line can be broken into two real valued equations. $$ \begin{aligned} a^5 - 10 \; a^3 b^2 + 5 \; a b^4 &= 1 \\ 5 \; a^4 b - 10 \; a^2 b^3 + b^5 &= 0 \\ \end{aligned} \tag {2} $$

First Solution

The second equation has a factor $b$ that can be factored out. $$ \begin{aligned} b \left( 5 \; a^4 - 10 \; a^2 b^2 + b^4 \right) &= 0 \\ \end{aligned} \tag {3} $$ When two factors multiply to zero, one or both of them have to be zero. $$ \begin{aligned} b = 0 \text{ or } 5 \; a^4 - 10 \; a^2 b^2 + b^4 &= 0 \\ \end{aligned} \tag {4} $$ The $b=0$ solution is the trivial first solution. From (1), since $a$ has to be real, it has to equal $1$, making $1+i0$ officially a solution.

Solve the Quadratic

The second factor is in a quadratic form. By dividing it through by $a^4$, the quadratic is on $(b/a)^2$. $$ \begin{aligned} 5 \; - 10 \; (b/a)^2 + (b/a)^4 &= 0 \\ \end{aligned} \tag {5} $$ The quadratic equation can then be applied. $$ \begin{aligned} (b/a)^2 &= \frac{ 10 \pm \sqrt{ 10^2 - 4\cdot1\cdot 5 } }{2} \\ &= \frac{ 10 \pm \sqrt{ 100 - 20 } }{2} \\ &= \frac{ 10 \pm \sqrt{ 80 } }{2} \\ &= 5 \pm \sqrt{ 20 } \\ &= 5 \pm 2 \sqrt{ 5 } \\ \end{aligned} \tag {6} $$ Then the square root is taken to get the simple ratio. $$ \begin{aligned} b/a &= \pm \sqrt{ 5 \pm 2 \sqrt{ 5 }} \\ \end{aligned} \tag {7} $$

Numeric Check of Slopes

Since there are two plus or minus signs, there are four possible values. $$ \begin{aligned} b/a &= \pm \sqrt{ 5 \pm 2 \cdot 2.236067977} \\ &= \pm \sqrt{ 5 \pm 4.472135955} \\ &= \pm \sqrt{ 9.472135955 \text{ or } 0.527864045 } \\ &= \pm \left[ 3.077683537 \text{ or } 0.726542528 \right] \\ \end{aligned} \tag {8} $$ The value of $a+i\;b$ on the complex plane corresponds to the point $(a,b)$ on the Cartesian plane. The slope of a line passing through the origin and the point is $b/a$. The slope of a line is also the tangent of its angle, so these values can be compared to the expected trigonometric values for the four non trivial solutions. Since the five Roots of Unity are spread evenly around the circle, the increment between each is $2\pi/5$. $$ \begin{aligned} \tan \left( \frac{2}{5} \pi \right) &= + \sqrt{ 5 + 2 \sqrt{ 5 }} \approx 3.077683537 \\ \tan \left( \frac{4}{5} \pi \right) &= - \sqrt{ 5 - 2 \sqrt{ 5 }} \approx -0.726542528 \\ \tan \left( \frac{6}{5} \pi \right) &= + \sqrt{ 5 - 2 \sqrt{ 5 }} \approx 0.726542528 \\ \tan \left( \frac{8}{5} \pi \right) &= - \sqrt{ 5 + 2 \sqrt{ 5 }} \approx -3.077683537 \\ \end{aligned} \tag {9} $$ The values match.

Slick Trick

Every derivation is better with a slick trick. Something pulled out of a hat to help. In this case, look what happens when you square this binomial: $$ \begin{aligned} \left( 1 \pm \sqrt{ 5 } \right)^2 &= 1 \pm 2 \sqrt{ 5 } + 5 \\ &= 1 + \left( 5 \pm 2 \sqrt{ 5 } \right) \\ &= 6 \pm 2 \sqrt{ 5 } \\ \end{aligned} \tag {10} $$ This allows (7) to be rewritten as: $$ \begin{aligned} b/a &= \pm \sqrt{ \left( 1 \pm \sqrt{ 5 } \right)^2 - 1^2 } \\ \end{aligned} \tag {11} $$ Then choosing the smaller of the two positive solutions. $$ \begin{aligned} b/a &= \sqrt{ \left( \sqrt{ 5 } - 1 \right)^2 - 1^2 } \\ \end{aligned} \tag {12} $$ The advantage of this form is that these values can be obtained by construction using a straight edge and a compass. The $\sqrt{5}$ can be obtained from a right triangle with a base of one and height of two. The value of $b/a$ can be obtained as the height of a right triangle with a hypothenuse of $\sqrt{5}-1$ and a base of one.

Choosing $\sqrt{5}+1$ instead leads to a different construction.

Construction

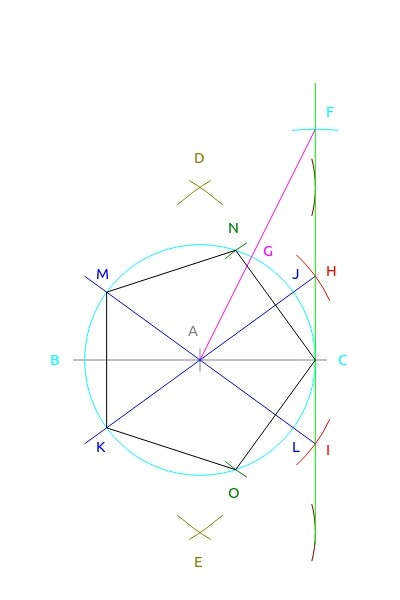
All drawing is done using the straight edge. Scribing is done using the compass. SPOILER ALERT: A rendition of the construction is in the appendix.

Step 1.  Draw horizontal axis and center hash
    Draw a horizontal line.  Then, in the center draw a
    short vertical hash line.  Label the intersection
    point 'A'.

Step 2.  Pick a radius and scribe a circle
    Set the compass with the point on 'A' and to a radius
    that will fit on the line.  Scribe a circle.  By
    definition, the radius is one.  The circle will
    intersect the horizontal line at two points.  Label
    the left on 'B' and the right one 'C'.

Step 3.  Draw perpendicular cross arcs
    Widen the compass so it is about 3/4 of the diameter
    or so.  Set the compass point on 'B' and scribe an
    arc above and below 'A'.  Repeat at point 'C'.
    There should be two X's formed.  Label the top one
    'D' and the bottom one 'E'.

Step 4.  Scribe arcs for tangent line
    Set the compass size to the radius of the circle.
    Then set the point on 'D' and scribe a vertical
    arc above point 'C'.  Do the same for 'E' below
    point 'C'.  The arcs should be in line with the
    right edge of the circle.

Step 5.  Draw tangent line
    Draw a tangent line to the two arcs and the right
    edge of the circle.  It needs to be extended
    upward to at least twice the circle radius.

Step 6.  Cross arc the tangent line at one diameter
    Set the compass point on 'C' and size it on the
    diameter at 'B'.  Scribe an arc on the tangent
    line above point 'C'.  Label the intersection
    point 'F'.

Step 7.  Connect to center
    Draw a line segment from 'F' to 'A'.  Label the
    point where the line intersects the circle as
    'G'.  The points 'ACF' now form a right triangle
    with a base of one unit and a height of two units.  

Step 8.  Scribe outer length onto tangent from center
    Set the compass width by the line segment 'GF'.
    Set the compass point on 'A' and scribe an arc
    above and below 'C' on the tangent line.  Label
    the intersection points 'H' and 'I'.

Step 9.  Draw lines from tangent marks through center and across
    Draw a line segment from 'H' through 'A' until
    the circle is crossed on the other side.  Label
    the right crossing point 'J' and the left crossing
    point as 'K'.
    Repeat for 'I' and label those points 'L' and
    'M' respectively.

Step 10.  Scribe edge marks
    Set the compass width using the points 'L' and
    'J'.  Set the compass point on 'C' and scribe an
    arc on the circle above and below.  Label the
    intersection points 'N' and 'O'.

Step 11.  Connect the marks for inscribed pentagon
    Draw the line segments 'CN', 'NM', 'MK', 'KO',
    and 'OC'.  The inscribed pentagon is complete.

Variations

Some of the steps are redundant. Point 'E' doesn't need to be made, nor its arc. However, having the longer span for the tangent line should improve expected accuracy. Likewise, 'I' (and 'L','M') need not have been drawn either. In that case, the edge distance can be marked by putting the point of the compass on 'J', spacing it to 'C', then scribing an arc at 'N'. Form there 'CN' could be copied around the circle.

Also, the line segments don't need to be fully drawn, only hashes where they cross the circle are needed.

Calculating the Point Values

Finding the actual values of the points is not that difficult. First we can find the corresponding complex value of 'J' by using similarity. 'J' is in the direction of 'H' having magnitude one. Therefore 'H' can be divided by its magnitude to get 'J'. $$ \begin{aligned} H = 1 + i \sqrt{ 5 - 2 \sqrt{ 5 }} \end{aligned} \tag {13} $$ It magnitude can be simplified by employing (10), which was the goal distance to have. $$ \begin{aligned} \| H \| = \sqrt{ 1^2 + \left( 5 - 2 \sqrt{ 5 } \right) } = \sqrt{ 6 - 2 \sqrt{ 5 } } = -1 + \sqrt{ 5 } \end{aligned} \tag {14} $$ Now, they can be divided and put in nicer form. $$ \begin{aligned} J &= \frac{H}{\| H \|} \\ &= \frac{1 + i \sqrt{ 5 - 2 \sqrt{ 5 }}}{-1 + \sqrt{ 5 }} \cdot \frac{1 + \sqrt{ 5 }}{1 + \sqrt{ 5 }} \\ &= \frac{(1 + \sqrt{ 5 }) + i \sqrt{ 5 - 2 \sqrt{ 5 }} \sqrt{ 6 + 2 \sqrt{ 5 } } }{-1 + 5 } \\ &= \frac{(1 + \sqrt{ 5 }) + i \sqrt{ 30 - 2 \sqrt{ 5 } - 20 }} {4} \\ &= \frac{1 + \sqrt{ 5 } }{4} + i \frac{\sqrt{ 10 - 2 \sqrt{ 5 } }}{4} \\ \end{aligned} \tag {15} $$ 'K' is on the opposite side of 'J', so its value is just the negative. 'M' is directly above 'K' and the same distance from the real axis so they are complex conjugates. $$ \begin{aligned} K &= -J = \frac{-1 - \sqrt{ 5 } }{4} - i \frac{\sqrt{ 10 - 2 \sqrt{ 5 } }}{4} \\ M &= K^* = \frac{-1 - \sqrt{ 5 } }{4} + i \frac{\sqrt{ 10 - 2 \sqrt{ 5 } }}{4} \\ \end{aligned} \tag {16} $$ This gives the left two points. Notice that 'O' is twice as far around the circle as 'M'. Therefore the 'O' value is the square of the 'M' value. $$ \begin{aligned} O &= M^2 \\ &= \left[ \frac{-\sqrt{ 6 + 2 \sqrt{ 5 } } }{4} + i \frac{\sqrt{ 10 - 2 \sqrt{ 5 } }}{4} \right]^2 \\ &= \left[\frac{ 6 + 2 \sqrt{ 5 } }{16} - \frac{10 - 2 \sqrt{ 5 } }{16} \right] - i\;2\left[ \frac{\sqrt{ (6 + 2 \sqrt{ 5 })(10 - 2 \sqrt{ 5 } )}}{16} \right] \\ &= \left[\frac{ -4 + 4 \sqrt{ 5 } }{16} \right] - i\;2\left[ \frac{\sqrt{ 60 + 8 \sqrt{ 5 } - 20 }}{16} \right] \\ &= \left[\frac{ -1 + \sqrt{ 5 } }{4} \right] - i\left[ \frac{\sqrt{ 10 + 2 \sqrt{ 5 } }}{4} \right] \\ \end{aligned} \tag {17} $$ The final point is simply the conjugate. $$ \begin{aligned} N = O^* &= \left[\frac{ -1 + \sqrt{ 5 } }{4} \right] + i\left[ \frac{\sqrt{ 10 + 2 \sqrt{ 5 } }}{4} \right] \\ \end{aligned} \tag {18} $$

Numeric Check of Points

Again, the angles of the five points around the circle are known, so their Cartesian coordinates can be determined by the Trigonometric functions, and the corresponding complex values thus determined. These can then be compared to the analytic solutions derived above. $$ \begin{aligned} \cos \left( \frac{2}{5} \pi \right) &= \cos \left( \frac{8}{5} \pi \right) = \frac{ -1 + \sqrt{ 5 } }{4} \approx 0.309016994 \\ \sin \left( \frac{2}{5} \pi \right) &= -\sin \left( \frac{8}{5} \pi \right) = \frac{\sqrt{ 10 + 2 \sqrt{ 5 } }}{4} \approx 0.951056516 \\ \end{aligned} \tag {19} $$ They match. $$ \begin{aligned} \cos \left( \frac{4}{5} \pi \right) &= \cos \left( \frac{6}{5} \pi \right) = \frac{-1 -\sqrt{ 5 } }{4} \approx -0.809016994 \\ \sin \left( \frac{4}{5} \pi \right) &= -\sin \left( \frac{6}{5} \pi \right) = \frac{\sqrt{ 10 - 2 \sqrt{ 5 } }}{4} \approx 0.587785252 \\ \end{aligned} \tag {20} $$ These also match.

Side Excursion

Notice that the decimal pattern matches in the first lines of (19) and (20). If you add them together the result is -0.5. This becomes understandable when the sum of all the cosines has to be zero, and the cosine for the trivial solution, being one, has been excluded. $$ \begin{aligned} \cos \left( \frac{2}{5} \pi \right) + \cos \left( \frac{4}{5} \pi \right) + \cos \left( \frac{6}{5} \pi \right) + \cos \left( \frac{8}{5} \pi \right) = -1 \end{aligned} \tag {21} $$ By symmetry. $$ \begin{aligned} \cos \left( \frac{2}{5} \pi \right) + \cos \left( \frac{4}{5} \pi \right) = \cos \left( \frac{6}{5} \pi \right) + \cos \left( \frac{8}{5} \pi \right) = -\frac{1}{2} \end{aligned} \tag {22} $$ This is confirmed by adding the analytical parts of (19) and (20). These parts can also be multiplied resulting in: $$ \begin{aligned} \cos \left( \frac{2}{5} \pi \right) \cos \left( \frac{4}{5} \pi \right) &= \frac{ -1 + \sqrt{ 5 } }{4} \cdot \frac{ -1 - \sqrt{ 5 } }{4}\\ &= \frac{ 1 - 5 }{16} = -\frac{1}{4} \end{aligned} \tag {23} $$ Returning to the left hand side and right hand side of (22), a different product can be produced by splitting the angle values into the average plus or minus the difference from average. $$ \begin{aligned} -\frac{1}{2} &= \cos \left( \frac{2}{5} \pi \right) + \cos \left( \frac{4}{5} \pi \right) \\ &= \cos \left( \frac{3}{5} \pi - \frac{1}{5} \pi \right) + \cos \left( \frac{3}{5} \pi + \frac{1}{5} \pi \right) \\ &= \cos \left( \frac{3}{5} \pi \right)\cos \left( \frac{1}{5} \pi \right) + \sin \left( \frac{3}{5} \pi \right)\sin \left( \frac{1}{5} \pi \right) \\ &+ \cos \left( \frac{3}{5} \pi \right)\cos \left( \frac{1}{5} \pi \right) - \sin \left( \frac{3}{5} \pi \right)\sin \left( \frac{1}{5} \pi \right) \\ &= 2 \cos \left( \frac{3}{5} \pi \right)\cos \left( \frac{1}{5} \pi \right) \\ \end{aligned} \tag {24} $$ Reversing the last line and solving. $$ \begin{aligned} \cos \left( \frac{3}{5} \pi \right)\cos \left( \frac{1}{5} \pi \right) &= -\frac{1}{4} \\ \end{aligned} \tag {25} $$ Just because we can, this is multiplied by (23). $$ \begin{aligned} \cos \left( \frac{1}{5} \pi \right)\cos \left( \frac{2}{5} \pi \right) \cos \left( \frac{3}{5} \pi \right)\cos \left( \frac{4}{5} \pi \right) &= \frac{1}{16} \\ \end{aligned} \tag {26} $$ And there is your fun fact for today. Finally, by symmetry: $$ \begin{aligned} \cos \left( \frac{1}{5} \pi \right) + \cos \left( \frac{2}{5} \pi \right) + \cos \left( \frac{3}{5} \pi \right) + \cos \left( \frac{4}{5} \pi \right) &= 0 \\ \end{aligned} \tag {27} $$ That is meant to leave you feeling centered.

Conclusion

Sometimes it's the Complex plane, sometimes it's the Cartesian plane, even sometimes the Polar, and sometimes an overlapping hybrid can be used. However, it is important to remember which representation you are working with and stick with the operations of that domain. Slopes don't really mean anything to complex numbers.

By doing a hybrid, the operations of geometric construction are matched with underlying numeric values from an analytic model.

In other words, another example of demonstrating math in context.

(Other articles are linked in my overview article. This one can be found in the "Fundamentals" section.)

Appendix - Construction Rendition

Sign in