Audio Decay Time (T60)
In audio, a decay by ![]() (one time-constant) is not enough to become inaudible, unless
the starting amplitude was extremely small.
In architectural acoustics (which includes the design of
concert halls [4]), a more commonly used measure of decay is ``
(one time-constant) is not enough to become inaudible, unless
the starting amplitude was extremely small.
In architectural acoustics (which includes the design of
concert halls [4]), a more commonly used measure of decay is ``![]() ''
(or T60), which is defined as the
time to decay by
''
(or T60), which is defined as the
time to decay by ![]() dB.4.7That is,
dB.4.7That is, ![]() is obtained by solving the equation
is obtained by solving the equation
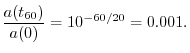
Next Section:
Circular Motion
Previous Section:
Why Exponentials are Important




















