Exponentials
The canonical form of an exponential function, as typically used in signal processing, is
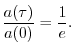
Why Exponentials are Important
Exponential decay occurs naturally when a quantity is decaying at a rate which is proportional to how much is left. In nature, all linear resonators, such as musical instrument strings and woodwind bores, exhibit exponential decay in their response to a momentary excitation. As another example, reverberant energy in a room decays exponentially after the direct sound stops. Essentially all undriven oscillations decay exponentially (provided they are linear and time-invariant). Undriven means there is no ongoing source of driving energy. Examples of undriven oscillations include the vibrations of a tuning fork, struck or plucked strings, a marimba or xylophone bar, and so on. Examples of driven oscillations include horns, woodwinds, bowed strings, and voice. Driven oscillations must be periodic while undriven oscillations normally are not, except in idealized cases.
Exponential growth occurs when a quantity is increasing at a rate proportional to the current amount. Exponential growth is unstable since nothing can grow exponentially forever without running into some kind of limit. Note that a positive time constant corresponds to exponential decay, while a negative time constant corresponds to exponential growth. In signal processing, we almost always deal exclusively with exponential decay (positive time constants).
Exponential growth and decay are illustrated in Fig.4.8.
Audio Decay Time (T60)
In audio, a decay by ![]() (one time-constant) is not enough to become inaudible, unless
the starting amplitude was extremely small.
In architectural acoustics (which includes the design of
concert halls [4]), a more commonly used measure of decay is ``
(one time-constant) is not enough to become inaudible, unless
the starting amplitude was extremely small.
In architectural acoustics (which includes the design of
concert halls [4]), a more commonly used measure of decay is ``![]() ''
(or T60), which is defined as the
time to decay by
''
(or T60), which is defined as the
time to decay by ![]() dB.4.7That is,
dB.4.7That is, ![]() is obtained by solving the equation
is obtained by solving the equation
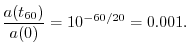
Next Section:
Complex Sinusoids
Previous Section:
Sinusoids








![\includegraphics[width=0.8 \twidth]{eps/exponential}](http://www.dsprelated.com/josimages_new/mdft/img441.png)
![\includegraphics[width=0.8\twidth]{eps/decaygrowth}](http://www.dsprelated.com/josimages_new/mdft/img442.png)












