Linear Phase Terms
The reason
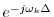 is called a linear phase term is
that its phase is a linear function of frequency:
is called a linear phase term is
that its phase is a linear function of frequency:
Thus, the
slope of the phase, viewed as a linear function of
radian-frequency
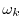
, is
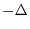
. In general, the
time
delay in samples equals
minus the slope of the linear phase
term. If we express the original
spectrum in polar form as
where
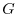
and
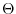
are the magnitude and phase of

, respectively
(both real), we can see that a linear phase term only modifies the
spectral
phase 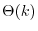
:
where

. A positive time delay (waveform shift to
the right) adds a
negatively sloped linear phase to the original
spectral phase. A negative time delay (waveform shift to the left) adds a
positively sloped linear phase to the original spectral phase. If we
seem to be belaboring this relationship, it is because it is one of the
most useful in practice.
Next Section: Linear Phase SignalsPrevious Section: Multiplication of Decimal Numbers
![]() is called a linear phase term is
that its phase is a linear function of frequency:
is called a linear phase term is
that its phase is a linear function of frequency:
![]() is called a linear phase term is
that its phase is a linear function of frequency:
is called a linear phase term is
that its phase is a linear function of frequency: