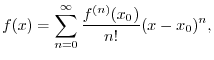A First Look at Taylor Series
Most ``smooth'' functions  can be expanded in the form of a
Taylor series expansion:
can be expanded in the form of a
Taylor series expansion:
This can be written more compactly as
where `
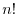
' is pronounced ``

factorial''.
An informal derivation of this formula for
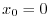
is given in
Appendix
E. Clearly, since many
derivatives are involved, a Taylor series expansion is only possible
when the function is so smooth that it can be differentiated again and
again. Fortunately for us, all audio
signals are in that category,
because
hearing is bandlimited
to below

kHz, and the audible
spectrum of any sum of
sinusoids is infinitely differentiable. (Recall
that

and
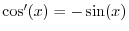
,
etc.). See §
E.6 for more about this point.
Next Section: Imaginary ExponentsPrevious Section: Real Exponents
![]() can be expanded in the form of a
Taylor series expansion:
can be expanded in the form of a
Taylor series expansion:

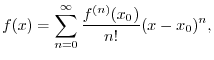
![]() can be expanded in the form of a
Taylor series expansion:
can be expanded in the form of a
Taylor series expansion: