Sign in
Search code
Ads
See Also
DSP Code Sharing > Resampling on arbitrary grid (vectorized)
Resampling on arbitrary grid (vectorized)
Language: Matlab
Processor: Not Relevant
Submitted by Markus Nentwig on Aug 14 2011
Licensed under a Creative Commons Attribution 3.0 Unported License
Resampling on arbitrary grid (vectorized)
Resamples a band-limited cyclic signal on an arbitrary grid via a vectorized evaluation of the Fourier series at the requested locations. The special case with signal energy at the Nyquist limit (-1, 1, -1, 1, ... component) is handled correctly.
The following two examples show resampling of two arbitrary signals:
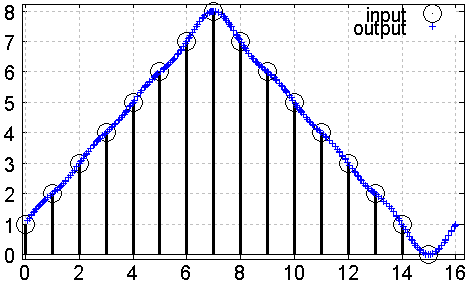
Fig. 1: Arbitrary signal example
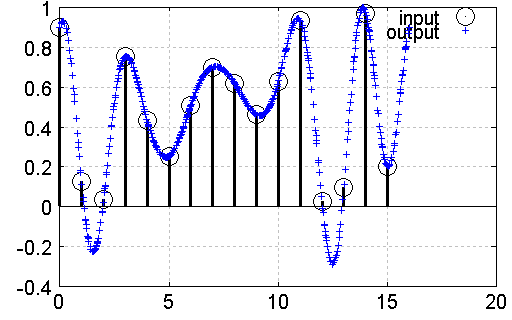
Fig. 2: Another example
The picture below illustrates the special case at the Nyquist limit:
Since the Fourier series coefficients are determined on a regular sampling grid, the outermost positive and negative frequencies are ambiguous.
The implementation provides some "interpretation" to resolve the ambiguity (using the additional constraint that a purely real-valued input signal should result in a purely real-valued output signal).
Fig. 3: Resampling a signal component at the Nyquist limit
A possible application is the generation of reference output signals for resampler design using least-mean-square methods, for example.
A related implementation that resamples on a regular grid (convert a n1-point cyclic signal to n2 samples) can be found here.
% Efficient resampling of a cyclic signal on an arbitrary grid
% M. Nentwig, 2011
% => calculates Fourier series coefficients
% => Evaluates the series on an arbitrary grid
% => takes energy exactly on the Nyquist limit into account (even-
% size special case)
% => The required matrix calculation is vectorized, but conceptually
% much more CPU-intensive than an IFFT reconstruction on a regular grid
% **************************************************************
close all; clear all;
% **************************************************************
% example signals
% **************************************************************
sig = [1 2 3 4 5 6 7 8 7 6 5 4 3 2 1 0];
%sig = repmat([1 -1], 1, 8); % highlights the special case at the Nyquist limit
%sig = rand(1, 16);
nIn = size(sig, 2);
% **************************************************************
% example resampling grid
% **************************************************************
evalGrid = rand(1, 500);
evalGrid = cumsum(evalGrid);
evalGrid = evalGrid / max(evalGrid) * nIn;
nOut = size(evalGrid, 2);
% **************************************************************
% determine Fourier series coefficients of signal
% **************************************************************
fCoeff = fft(sig);
nCoeff = 0;
if mod(nIn, 2) == 0
% **************************************************************
% special case for even-sized length: There is ambiguity, whether
% the bin at the Nyquist limit corresponds to a positive or negative
% frequency. Both give a -1, 1, -1, 1, ... waveform on the
% regular sampling grid.
% This coefficient will be treated separately. Effectively, it will
% be interpreted as being half positive, half negative frequency.
% **************************************************************
bin = floor(nIn / 2) + 1;
nCoeff = fCoeff(bin);
fCoeff(bin) = 0; % remove it from the matrix-based evaluation
end
% **************************************************************
% indices for Fourier series
% since evaluation does not take place on a regular grid,
% one needs to distinguish between negative and positive frequencies
% **************************************************************
o = floor(nIn/2);
k = 0:nIn-1;
k = mod(k + o, nIn) - o;
% **************************************************************
% m(yi, xi) = exp(2i * pi * evalGrid(xi) * k(yi))
% each column of m evaluates the series for one requested output location
% **************************************************************
m = exp(2i * pi * transpose(repmat(transpose(evalGrid / nIn), 1, nIn) ...
* diag(k))) / nIn;
% each output point is the dot product between the Fourier series
% coefficients and the column in m that corresponds to the location of
% the output point
out = fCoeff * m;
out = out + nCoeff * cos(pi*evalGrid) / nIn;
% **************************************************************
% plot
% **************************************************************
out = real(out); % chop off roundoff error for plotting
figure(); grid on; hold on;
h = stem((0:nIn-1), sig, 'k'); set(h, 'lineWidth', 3);
h = plot(evalGrid, out, '+'); set(h, 'markersize', 2);
legend('input', 'output');
title('resampling of cyclic signal on arbitrary grid');
posted by Markus Nentwig Markus received his Dipl. Ing. degree in electrical engineering / communications in 1999. Work interests include RF transceiver system design, implementation, modeling and verification. He works as senior architect for Renesas Mobile Europe in Finland.
Comments
No comments yet for this code