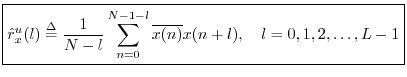Autocorrelation

The cross-correlation of a signal with itself gives its autocorrelation:

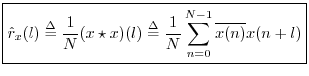
$\displaystyle \zbox {{\hat r}_x(l) \isdef \frac{1}{N}(x\star x)(l) \isdef \frac{1}{N}\sum_{n=0}^{N-1}\overline{x(n)} x(n+l)}$

The autocorrelation function is Hermitian:

$\displaystyle {\hat r}_x(-l) = \overline{{\hat r}_x(l)}$

When

is real, its autocorrelation is real and even (symmetric about lag zero).

The unbiased cross-correlation similarly reduces to an unbiased autocorrelation when $x\equiv y$ :

$\displaystyle \zbox {{\hat r}^u_x(l) \isdef \frac{1}{N-l}\sum_{n=0}^{N-1-l} \overline{x(n)} x(n+l),\quad l = 0,1,2,\ldots,L-1} \protect$

(8.2)

The DFT of the true autocorrelation function $r_x(n)\in{\bf R}^N$ is the (sampled) power spectral density (PSD), or power spectrum, and may be denoted

$\displaystyle R_x(\omega_k) \isdef \hbox{\sc DFT}_k(r_x).$

The complete (not sampled) PSD is $R_x(\omega) \isdef \hbox{\sc DTFT}_k(r_x)$ , where the DTFT is defined in Appendix B (it's just an infinitely long DFT). The DFT of ${\hat r}_x$ thus provides a sample-based estimate of the PSD:^8.7

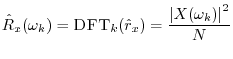
$\displaystyle {\hat R}_x(\omega_k)=\hbox{\sc DFT}_k({\hat r}_x) = \frac{\left\vert X(\omega_k)\right\vert^2}{N}$

We could call ${\hat R}_x(\omega_k)$ a ``sampled sample power spectral density''.

At lag zero, the autocorrelation function reduces to the average power (mean square) which we defined in §5.8:

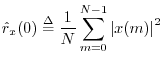
$\displaystyle {\hat r}_x(0) \isdef \frac{1}{N}\sum_{m=0}^{N-1}\left\vert x(m)\right\vert^2 % \isdef \Pscr_x^2$

Replacing ``correlation'' with ``covariance'' in the above definitions gives corresponding zero-mean versions. For example, we may define the sample circular cross-covariance as

$\displaystyle \zbox {{\hat c}_{xy}(n) \isdef \frac{1}{N}\sum_{m=0}^{N-1}\overline{[x(m)-\mu_x]} [y(m+n)-\mu_y].}$

where $\mu_x$ and $\mu_y$ denote the means of

and

, respectively. We also have that ${\hat c}_x(0)$ equals the sample variance of the signal

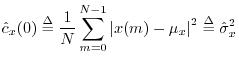
$\displaystyle {\hat c}_x(0) \isdef \frac{1}{N}\sum_{m=0}^{N-1}\left\vert x(m)-\mu_x\right\vert^2 \isdef {\hat \sigma}_x^2$

Order a Hardcopy of Mathematics of the DFT

Previous: Unbiased Cross-Correlation
Next: Matched Filtering

written by Julius Orion Smith III
Julius Smith's background is in electrical engineering (BS Rice 1975, PhD Stanford 1983). He is presently Professor of Music and Associate Professor (by courtesy) of Electrical Engineering at Stanford's Center for Computer Research in Music and Acoustics (CCRMA), teaching courses and pursuing research related to signal processing applied to music and audio systems. See http://ccrma.stanford.edu/~jos/ for details.

Sign in

Search Online Books

Free Online Books

Ads

Chapters

See Also

Mathematics of the DFT
    Example Applications of the DFT
       Correlation Analysis
          Autocorrelation