Sample Power Spectral Density
The Fourier transform of the sample autocorrelation function
![]() (see (6.6)) is defined as the
sample power spectral density (PSD):
(see (6.6)) is defined as the
sample power spectral density (PSD):
 |
(7.11) |
This definition coincides with the classical periodogram when
Similarly, the true power spectral density of a stationary stochastic
processes ![]() is given by the Fourier transform of the true
autocorrelation function
is given by the Fourier transform of the true
autocorrelation function ![]() , i.e.,
, i.e.,
| (7.12) |
For real signals, the autocorrelation function is always real and
even, and therefore the power spectral density is real and even for
all real signals.
An area under the PSD,
![]() , comprises the contribution to the
variance of
, comprises the contribution to the
variance of ![]() from the frequency interval
from the frequency interval
![]() . The total integral of the PSD gives
the total variance:
. The total integral of the PSD gives
the total variance:
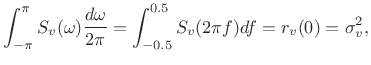 |
(7.13) |
again assuming
Since the sample autocorrelation of white noise approaches an impulse, its PSD approaches a constant, as can be seen in Fig.6.1. This means that white noise contains all frequencies in equal amounts. Since white light is defined as light of all colors in equal amounts, the term ``white noise'' is seen to be analogous.
Next Section:
Biased Sample Autocorrelation
Previous Section:
Sample Autocorrelation




















