Convolution Theorem for the DTFT
The convolution of discrete-time signals ![]() and
and ![]() is defined
as
is defined
as
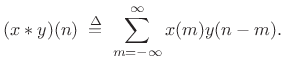 |
(3.22) |
This is sometimes called acyclic convolution to distinguish it from the cyclic convolution used for length
The convolution theorem is then
| (3.23) |
That is, convolution in the time domain corresponds to pointwise multiplication in the frequency domain.
Proof: The result follows immediately from interchanging the order
of summations associated with the convolution and DTFT:
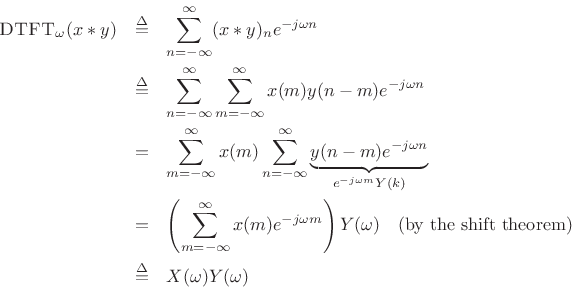
Next Section:
Correlation Theorem for the DTFT
Previous Section:
Shift Theorem for the DTFT




















