Free Books    Spectral Audio Signal Processing  

Continuous Wavelet Transform

In the present (Hilbert space) setting, we can now easily define the continuous wavelet transform in terms of its signal basis set:

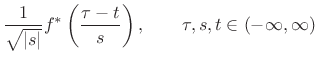$\displaystyle \displaystyle \varphi_{s\tau}(t)$ $\displaystyle \isdef$ $\displaystyle \frac{1}{\sqrt{\vert s\vert}} f^\ast\left(\frac{\tau-t}{s}\right), \qquad \tau,s,t \in (-\infty,\infty)$  
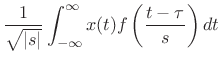$\displaystyle X(s,\tau)$ $\displaystyle \isdef$ $\displaystyle \frac{1}{\sqrt{\vert s\vert}} \int_{-\infty}^{\infty} x(t) f\left(\frac{t-\tau}{s}\right) dt$  

The parameter $ s$ is called a scale parameter (analogous to frequency). The normalization by $ 1/\sqrt{\vert s\vert}$ maintains energy invariance as a function of scale. We call $ X(s,\tau)$ the wavelet coefficient at scale $ s$ and time $ \tau$ . The kernel of the wavelet transform $ f(t)$ is called the mother wavelet, and it typically has a bandpass spectrum. A qualitative example is shown in Fig.11.31.

Figure: Typical qualitative appearance of first three wavelets when the scale parameter is $ s=2$ .
\includegraphics[width=0.8\twidth]{eps/wavelets}

The so-called admissibility condition for a mother wavelet $ \psi(t)$ is

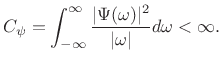
$\displaystyle C_\psi = \int_{-\infty}^\infty \frac{\vert\Psi(\omega )\vert^2}{\vert\omega \vert}d\omega < \infty . $

Given sufficient decay with $ \omega$ , this reduces to $ \Psi(0)=0$ , that is, the mother wavelet must be zero-mean.

The Morlet wavelet is simply a Gaussian-windowed complex sinusoid:

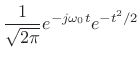$\displaystyle \psi(t)$ $\displaystyle \isdef$ $\displaystyle \frac{1}{\sqrt{2\pi}} e^{-j\omega _0 t} e^{-t^2/2}$  
$\displaystyle \;\longleftrightarrow\;\quad \Psi(\omega )$ $\displaystyle =$ $\displaystyle e^{-(\omega -\omega _0)^2/2}$  

The scale factor is chosen so that $ \left\Vert\,\psi\,\right\Vert=1$ . The center frequency $ \omega_0$ is typically chosen so that second peak is half of first:

$\displaystyle \omega _0\eqsp \pi\sqrt{2/\hbox{ln}2} \;\approx\; 5.336$ (12.119)

In this case, we have $ \Psi(0)\approx 7\times10^{-7}\approx 0$ , which is close enough to zero-mean for most practical purposes.

Since the scale parameter of a wavelet transform is analogous to frequency in a Fourier transform, a wavelet transform display is often called a scalogram, in analogy with an STFT ``spectrogram'' (discussed in §7.2).

When the mother wavelet can be interpreted as a windowed sinusoid (such as the Morlet wavelet), the wavelet transform can be interpreted as a constant-Q Fourier transform.12.5Before the theory of wavelets, constant-Q Fourier transforms (such as obtained from a classic third-octave filter bank) were not easy to invert, because the basis signals were not orthogonal. See Appendix E for related discussion.

Next Section:
Discrete Wavelet Transform
Previous Section:
Normalized STFT Basis