DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Relation of Smoothness to Roll-Off Rate

In §3.1.1, we found that the side lobes of the rectangular-window transform ``roll off'' as $ 1/\omega$ . In this section we show that this roll-off rate is due to the amplitude discontinuity at the edges of the window. We also show that, more generally, a discontinuity in the $ n$ th derivative corresponds to a roll-off rate of $ 1/\omega^{n+1}$ .

The Fourier transform of an impulse $ x(t)=\delta(t)$ is simply

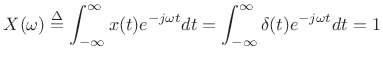$\displaystyle X(\omega)\isdef \int_{-\infty}^\infty x(t)e^{-j\omega t}dt = \int_{-\infty}^\infty \delta(t)e^{-j\omega t}dt = 1$ (B.70)

by the sifting property of the impulse under integration. This shows that an impulse consists of Fourier components at all frequencies in equal amounts. The roll-off rate is therefore zero in the Fourier transform of an impulse.

By the differentiation theorem for Fourier transforms (§B.2), if $ x\;\leftrightarrow\;X$ , then

$\displaystyle {\cal F}_\omega\{{\dot x}\} = j\omega X(\omega),$ (B.71)

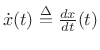where $ {\dot x}(t)\isdef \frac{dx}{dt}(t)$ . Consequently, the integral of $ x(t)$ transforms to $ X(\omega)/(j\omega)$ :

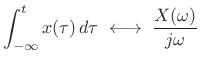$\displaystyle \int_{-\infty}^t x(\tau)\,d\tau \;\longleftrightarrow\;\frac{X(\omega)}{j\omega}$ (B.72)

The integral of the impulse is the unit step function:

$\displaystyle \int_{-\infty}^t \delta(\tau)\,d\tau = u(t) \isdef \left\{\begin{array}{ll} 1, & t\geq0 \\ [5pt] 0, & t<0 \\ \end{array} \right.$ (B.73)

Therefore,B.4

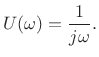$\displaystyle U(\omega) = \frac{1}{j\omega}.$ (B.74)

Thus, the unit step function has a roll-off rate of $ -6$ dB per octave, just like the rectangular window. In fact, the rectangular window can be synthesized as the superposition of two step functions:

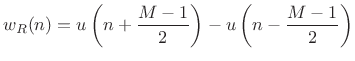$\displaystyle w_R(n) = u\left(n+\frac{M-1}{2}\right) - u\left(n-\frac{M-1}{2}\right)$ (B.75)

Integrating the unit step function gives a linear ramp function:

$\displaystyle \int_{-\infty}^t u(\tau)d\tau = t \cdot u(t) = \left\{\begin{array}{ll} t, & t\geq0 \\ [5pt] 0, & t<0 \\ \end{array} \right..$ (B.76)

Applying the integration theorem again yields

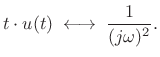$\displaystyle t\cdot u(t) \;\longleftrightarrow\;\frac{1}{(j\omega)^2}.$ (B.77)

Thus, the linear ramp has a roll-off rate of $ -12$ dB per octave. Continuing in this way, we obtain the following Fourier pairs:

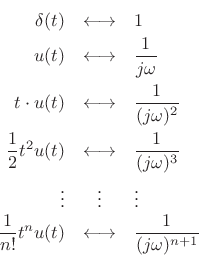
\begin{eqnarray*} \delta(t) &\longleftrightarrow& 1\\ u(t) &\longleftrightarrow& \frac{1}{j\omega}\\ t\cdot u(t) &\longleftrightarrow& \frac{1}{(j\omega)^2}\\ \frac{1}{2}t^2 u(t) &\longleftrightarrow& \frac{1}{(j\omega)^3}\\ \vdots & \vdots & \vdots \\ \frac{1}{n!}t^n u(t) &\longleftrightarrow& \frac{1}{(j\omega)^{n+1}} \end{eqnarray*}

Now consider the Taylor series expansion of the function $ x(t) = t^n u(t)$ at $ t=0$ :

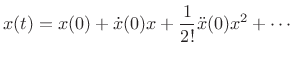$\displaystyle x(t) = x(0) + {\dot x}(0) x + \frac{1}{2!}{\ddot x}(0) x^2 + \cdots$ (B.78)

The derivatives up to order $ n-1$ are all zero at $ t=0$ . The $ n$ th derivative, however, has a discontinuous jump at $ t=0$ . Since this is the only ``wideband event'' in the signal, we may conclude that a discontinuity in the $ n$ th derivative corresponds to a roll-off rate of $ 1/\omega^{n+1}$ . The following theorem generalizes this result to a wider class of functions which, for our purposes, will be spectrum analysis window functions (before sampling):


Theorem: (Riemann Lemma): If the derivatives up to order $ n$ of the function $ w(t)$ exist and are of bounded variation (defined below), then its Fourier Transform $ W(\omega)$ is asymptotically of orderB.5 $ 1/\omega^{n+1}$ , i.e.,

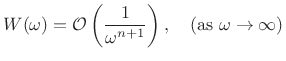$\displaystyle W(\omega) = {\cal O}\left(\frac{1}{\omega^{n+1}}\right), \quad(\hbox{as }\omega\to\infty)$ (B.79)

Proof: Following [202, p. 95], let $ w(t)$ be any real function of bounded variation on the interval $ (a,b)$ of the real line, and let

$\displaystyle w(t) = w_{\scriptscriptstyle\uparrow}(t) - w_{\scriptscriptstyle\downarrow}(t)$ (B.80)

denote its decomposition into a nondecreasing part $ w_{\scriptscriptstyle\uparrow}(t)$ and nonincreasing part $ -w_{\scriptscriptstyle\downarrow}(t)$ .B.6 Then there exists $ \tau\in(a,b)$ such that

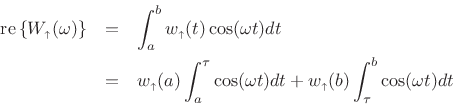
\begin{eqnarray*} \mbox{re}\left\{W_{\scriptscriptstyle\uparrow}(\omega)\right\} &=& \int_a^b w_{\scriptscriptstyle\uparrow}(t)\cos(\omega t) dt \\ &=& w_{\scriptscriptstyle\uparrow}(a)\int_a^\tau \cos(\omega t) dt + w_{\scriptscriptstyle\uparrow}(b)\int_\tau^b \cos(\omega t) dt \end{eqnarray*}

Since

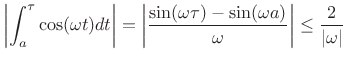$\displaystyle \left\vert\int_a^\tau\cos(\omega t) dt\right\vert = \left\vert\frac{\sin(\omega \tau) - \sin(\omega a)}{\omega}\right\vert \leq \frac{2}{\vert\omega\vert}$ (B.82)

we conclude

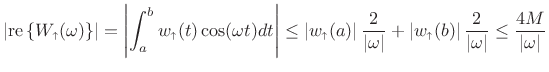$\displaystyle \left\vert\mbox{re}\left\{W_{\scriptscriptstyle\uparrow}(\omega)\right\}\right\vert = \left\vert\int_a^b w_{\scriptscriptstyle\uparrow}(t)\cos(\omega t) dt \right\vert \leq \left\vert w_{\scriptscriptstyle\uparrow}(a)\right\vert\frac{2}{\vert\omega\vert} + \left\vert w_{\scriptscriptstyle\uparrow}(b)\right\vert\frac{2}{\vert\omega\vert} \leq \frac{4M}{\left\vert\omega\right\vert}$ (B.83)

where 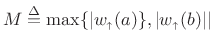$ M\isdef \max\{\left\vert w_{\scriptscriptstyle\uparrow}(a)\},\left\vert w_{\scriptscriptstyle\uparrow}(b)\right\vert\right\vert$ , which is finite since $ w$ is of bounded variation. Note that the conclusion holds also when $ (a,b)=(-\infty,\infty)$ . Analogous conclusions follow for im$ \left\{W_{\scriptscriptstyle\uparrow}(\omega)\right\}$ , re$ \left\{w_{\scriptscriptstyle\downarrow}(\omega)\right\}$ , and im$ \left\{w_{\scriptscriptstyle\downarrow}(\omega)\right\}$ , leading to the result

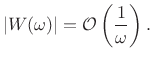$\displaystyle \left\vert W(\omega)\right\vert = {\cal O}\left(\frac{1}{\omega}\right).$ (B.84)

If in addition the derivative $ w^\prime (t)$ is bounded on $ (a,b)$ , then the above gives that its transform $ j\omega W(\omega)$ is asymptotically of order $ 1/\omega$ , so that $ W(\omega) = {\cal O}(1/\omega^2)$ . Repeating this argument, if the first $ n$ derivatives exist and are of bounded variation on $ (a,b)$ , we have $ W(\omega) = {\cal O}(1/\omega^{n+1})$ . $ \Box$

Since spectrum-analysis windows $ w(n)$ are often obtained by sampling continuous time-limited functions $ w(t)$ , we normally see these asymptotic roll-off rates in aliased form, e.g.,

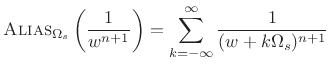$\displaystyle \hbox{\sc Alias}_{\Omega_s}\left(\frac{1}{w^{n+1}}\right) = \sum_{k=-\infty}^\infty\frac{1}{(w+k\Omega_s)^{n+1}}$ (B.85)

where $ \Omega_s=2\pi f_s$ denotes the sampling rate in radians per second. This aliasing normally causes the roll-off rate to ``slow down'' near half the sampling rate, as shown in Fig.3.6 for the rectangular window transform. Every window transform must be continuous at $ \omega=\pm\pi$ (for finite windows), so the roll-off envelope must reach a slope of zero there.

In summary, we have the following Fourier rule-of-thumb:

$\displaystyle \zbox {\hbox{$n$\ derivatives} \;\longleftrightarrow\;-6(n+1) \hbox{ dB per octave roll-off rate}}$ (B.86)

This is also $ -20(n+1)$ dB per decade.

To apply this result to estimating FFT window roll-off rate (as in Chapter 3), we normally only need to look at the window's endpoints. The interior of the window is usually differentiable of all orders. For discrete-time windows, the roll-off rate ``slows down'' at high frequencies due to aliasing.

Next Section:
Random Variables & Stochastic Processes
Previous Section:
The Uncertainty Principle