The equation error is defined (in the frequency domain) as
By comparison, the more natural frequency-domain error
is the so-called output error:
The names of these errors make the most sense in the time domain. Let
 and
and  denote the filter input and output, respectively, at time
denote the filter input and output, respectively, at time
 . Then the equation error is the error in the difference equation:
. Then the equation error is the error in the difference equation:
while the output error is the difference between the ideal and approximate
filter outputs:
Denote the 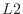 norm of the equation error by
norm of the equation error by
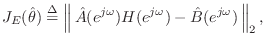 |
(I.11) |
where
![$ \hat{\theta}^T = [\hat{b}_0,\hat{b}_1,\ldots,\hat{b}_{{n}_b}, \hat{a}_1,\ldots, \hat{a}_{{n}_a}]$](http://www.dsprelated.com/josimages_new/filters/img2401.png)
is the
vector of unknown filter coefficients. Then the problem is to minimize
this norm with respect to
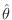
. What makes the equation-error so easy to
minimize is that it is
linear in the parameters. In the time-domain
form, it is clear that the equation error is linear in the unknowns
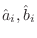
. When the error is linear in the parameters, the sum of
squared errors is a
quadratic form which can be minimized using one
iteration of
Newton's method. In other words, minimizing the
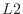
norm of
any error which is linear in the parameters results in a set of linear
equations to solve. In the case of the equation-error minimization at
hand, we will obtain
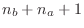
linear equations in as many unknowns.
Note that (I.11) can be expressed as
Thus, the equation-error can be interpreted as a
weighted output
error in which the frequency weighting function on the unit circle is
given by
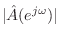
. Thus, the weighting function is determined
by the filter
poles, and the error is weighted
less near the
poles. Since the poles of a good
filter-design tend toward regions of
high spectral energy, or toward ``irregularities'' in the
spectrum, it is
evident that the equation-error criterion assigns less importance to the
most prominent or structured spectral regions. On the other hand, far away
from the roots of
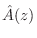
, good fits to
both phase and magnitude can
be expected. The weighting effect can be eliminated through
use of the
Steiglitz-McBride algorithm
[
45,
78] which iteratively solves the weighted
equation-error solution, using the canceling weight function from the
previous iteration. When it converges (which is typical in practice), it
must converge to the output error minimizer.
Next Section: Error Weighting and Frequency WarpingPrevious Section: Examples
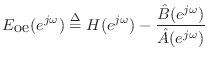
![]() and
and ![]() denote the filter input and output, respectively, at time
denote the filter input and output, respectively, at time
![]() . Then the equation error is the error in the difference equation:
. Then the equation error is the error in the difference equation:
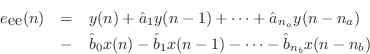
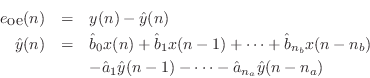
![]() norm of the equation error by
norm of the equation error by



















