Handling Spectral Inversion in Baseband Processing
The problem of "spectral inversion" comes up fairly frequently in the context of signal processing for communication systems. In short, "spectral inversion" is the reversal of the orientation of the signal bandwidth with respect to the carrier frequency. Rick Lyons' article on "Spectral Flipping" at http://www.dsprelated.com/showarticle/37.php discusses methods of handling the inversion (as shown in Figure 1a and 1b) at the signal center frequency. Since most communication systems process the signal at baseband rather than at RF or IF frequencies, this article discusses techniques that can be applied at baseband. The differences in the various techniques often result in a "Huh?" from many people, and this article will attempt to address the concepts behind the techniques in a way that clarifies the methodologies.
Spectral inversion happens as a result of mixing processes in RF or IF electronics. Systems using direct conversion from baseband to Radio Frequency are less susceptible to this problem as long as the transmitters and receivers follow the same conventions on mixing. In other words, for example, all transmitters mix the signal up to RF by multiplying by ejωt and mix the signal down by multiplying by e-jωt. Even this can be confused in implementation, however, as we shall see later. Systems that first mix the transmit signal to an IF frequency and then to RF, however, have more opportunities to invert the spectrum.
The use of an Intermediate Frequency before mixing the signal to the final Radio Frequency is often useful, especially in modular equipment. Many satellite and terrestrial data links use modems have an interface at a 70MHz IF. This allows operators to purchase the modem and the radio unit separately, so that a modem can be applied generically to various bands or applications by selecting a radio unit and antenna at the desired band. Since there is general industry standardization for the IF frequency to be at 70MHz for such equipment, radio units at different bands can be mixed and matched to modems using the same IF frequency.
Since the signal at the IF frequency is real-valued, mixing it to a different RF frequency involves multiplication by a sinusoid rather than a complex vector. Multiplying (or mixing) two sinusoids results in both a high and a low frequency result, mathematically expressed as
y(t) = sin(ω1t)sin(ω2t) = sin((ω1+ω2)t)+sin((ω1-ω2)t) (1)
where ω1 and ω2 are the frequencies of the mixing signals. If ω1 corresponds to the 70MHz IF frequency and the desired Radio Frequency is, for example 1.5GHz, then the mixing frequency, ω2, can be either 1.5GHz+70MHz (a low-side mix) or 1.5GHz-70MHz (a high-side mix). The result puts a mixed signal at 1.5GHz and an extraneous mixing product at 2x70MHz either above or below the desired output. It is the radio designer's job, and usually discretion, to choose either a high-side or low-side mix architecture and design a filter to remove the extraneous mixing product at the output. Whether a high-side or a low-side mix is chosen is an implementation detail that may be driven by cost, performance, available real-estate, spurious emission concerns, filtering solutions, or a number of factors. It could even be, and is sometimes the case, that the radio architect uses multiple mixing stages to get from the IF frequency to the desired RF frequency, especially if the RF frequency is very high. At each stage a decision must be made whether to use a high-side or low-side mix.
A block diagram of an example modulator and mixing chain is shown in Figure 1. The modulator generates an I and Q pair at baseband which is then mixed up to a 70MHz IF frequency. The complex reference signal in this case is generated by a DDS/NCO (two names for the same thing). Not shown is the Digital to Analog Conversion, which could be done to the I and Q signals at baseband or after the first mix to the 70MHz IF frequency. The implementation details, such as the point of DAC conversion, do not change the general block diagram. The IF bandpass signal is real-valued and mixes with a sinusoid with a frequency of 1430MHz. The product of this mixing process is then filtered to reject the low-side image so that the desired high-side signal at 1500MHz remains.
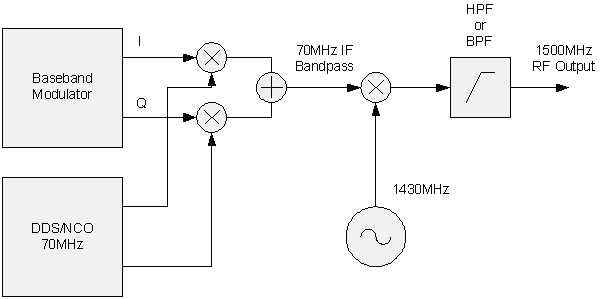
Figure 1. Block diagram of an example baseband modulator and mixing stages up to 1500MHz. A 70MHz IF signal is generated which is then mixed up to 1500MHz.
A spectral representation of the mixing process shown in Figure 1 appears in Figure 2. The 70MHz IF signal is translated to the 1500MHz RF frequency via a single-stage mix. The low-side spectrum at 1360MHz is inverted, while the high-side spectrum is not.
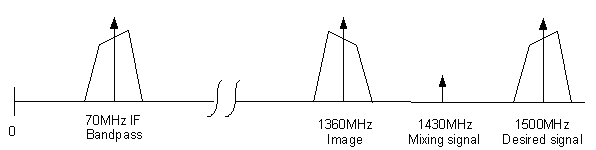
Figure 2. Shown is a spectral representation of a 70MHz IF bandpass signal and the result of mixing it with a 1430MHz sinusoid. The high-side desired signal at 1500MHz is not inverted, but the image at 1360MHz is inverted.
For the case shown in Figures 1 and 2 the output spectrum is not inverted with respect to the 70MHz IF signal since the sum image is used for the output rather than the difference. It is easy to see that if the reference oscillator frequency were changed to 1570MHz, that the low-side image would be at the desired 1500MHz frequency and the high-side image at 1640MHz would need to be filtered out. It could be that the stages shown are just the first in a chain of mixes used to get the signal to a much higher frequency, say 22GHz, before final transmission. Depending upon the design constraints and the desired frequencies there may be significant advantages to taking either a high-side or low-side product at various mixing stages. Likewise for some deployments there may be a chain of separate pieces of equipment cabled together between the modem and the antenna to achieve mixing, multiplexing, switching, or other system requirements. If the number of low-side mixing products used in the chain is not even, then the output spectrum will be inverted.
The result of all this is that there is often an ambiguity in the receiver that must be resolved, i.e., has the spectrum been inverted or not? There is often no practical way to guarantee how many mixing stages or inversions the signal has undergone between the baseband modulator and the baseband demodulator. While many demodulators can acquire and synchronize to a signal with inverted spectrum, the recovered data will likely appear to be garbage to the Forward Error Correction or downstream processing. Understanding why this is true is key to understanding spectral inversion and how to deal with it in baseband processing.
Consider a component of a baseband signal at 10MHz above the center frequency. In the mixing products after a complex mix or in the high-side sum image the 10MHz baseband component will still be 10MHz above the center frequency. However, as (1) shows, the low-side image is the difference of the frequencies present and the reference oscillator frequency. After the first mix to the 70MHz IF, the 10MHz component will be at 80MHz. The difference between the 1430MHz reference and the 80MHz component puts the component at 1430-80 = 1350MHz, or 10MHz below the center of the low-side image. Figure 3 illustrates this graphically.
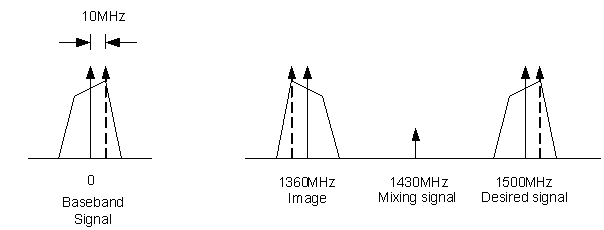
Figure 3. Detailed view of the spectral inversion with respect to a component of the baseband signal at 10MHz. In the difference image the component at +10MHz in the baseband signal appears ten megahertz below the carrier frequency.
If the inverted spectrum were translated back to baseband without any additional inversions, the component that was at +10MHz in the modulator baseband signal will be at -10MHz in the demodulator baseband. In other words, all the frequencies in the baseband signal will have experience a sign inversion, so frequencies that were positive will be negative and frequencies that were negative will be positive. In the baseband representation with I and Q components, this can be conceptualized as a reverse in direction of rotation of the complex vector. Figure 4 is borrowed, with permission, from [1], and shows a complex rotating vector. As show, from a strict interpretation of the axes definitions, the vector is rotating counterclockwise, as shown projected on the imaginary plane at the rear of the diagram. This is consistent with what would be described by an observer at arrow B. It should be noted, however, that an observer looking from the perspective of arrow A would see the vector rotating in a clockwise direction. This difference in perspective can be used to "invert" the spectrum easily at baseband.
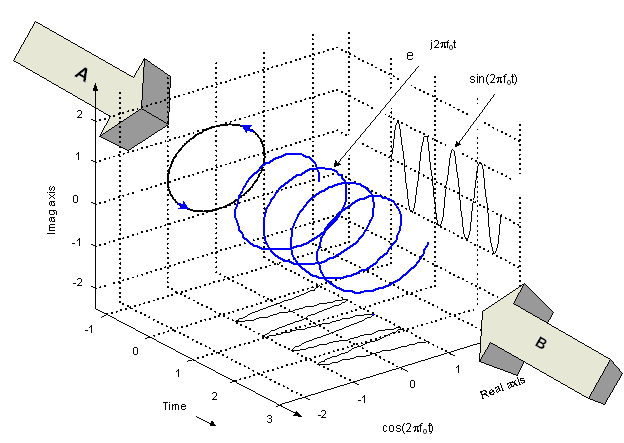
Figure 4. A complex vector rotating in time produces a helical trace. The sinusoidal components are shown projected on the real and imaginary planes, and the circular trace is shown projected on the rear, complex plane. Whether the vector is rotating clockwise or counterclockwise will change when viewed from the perspective of the A arrow or the B arrow. The basic diagram shown is used, with permission, from [1]. The arrows have been added here.
From a mathematical perspective, the desire is to be able to easily invert the sign of the frequency of all of the components of the signal. In other words, change ejωt to e-jωt. We can observe from Euler's equation that
ejωt = cos(ωt) + jsin(ωt) (2)
and the simple spectral inversion of the same
e-jωt = cos(-ωt) + jsin(-ωt) (3)
Remembering the basic trigonometric identities
sin(-q) = -sin(q) (4)
cos(-q) = cos(q) (5)
we can rewrite (3) as:
e-jωt = cos(ωt) - jsin(ωt) (6)
Using the symmetry and shift formulas,
sin(q +p/2) = cos(q) (7)
cos(q +p/2) = -sin(q) (8)
Since we are only interested in the direction of rotation and not the absolute phase, we can add an arbitrary initial phase of p/2 and write
e-jωt+p/2 = cos(-ωt+p/2) + jsin(-ωt+p/2)
= -sin(-ωt) + jcos(-ωt)
= sin(ωt) + jcos(ωt) (9)
Additionally,
sin(p+/-q) = -/+sin(q) (10)
cos(p+/-q) = -cos(q) (11)
lets us add an initial phase of p and write
e-jωt+p = cos(-ωt+p) + jsin(-ωt+p)
= -cos(ωt) - jsin(-ωt)
= -cos(ωt) + jsin(ωt) (12)
In summary, we have three expressions for writing forms of e-jωt in terms of sin and cos with arguments of positive ωt, specifically:
e-jωt = cos(ωt) - jsin(ωt) (6)
e-jωt+p/2 = sin(ωt) + jcos(ωt) (9)
e-jωt+p = -cos(ωt) + jsin(ωt) (12)
Assigning, arbitrarily, the demodulator I channel to the first, cos-related term, and the Q channel to the second, sin-related (or imaginary) axis such that after downconversion of the modulated signal x(t) by ejωt we have
x(t)ejωt = x(t)(cos(ωt) + jsin(ωt))
= I(t) + jQ(t) (13)
Applying (6), (9) and (12) we have
x(t)e-jωt = I(t) - jQ(t) (14)
x(t)e-jwt+p/2 = Q(t) + jI(t) (15)
x(t)e-jwt+p = -I(t) + jQ(t) (16)
Interpreting this mathematically we have three different means of inverting the spectrum at baseband in the demodulator,
1. Invert the Q channel (14)
2. Swap the I and Q channels (15)
3. Invert the I channel (16)
The addition of the arbitrary phase terms for (15) and (16) is not problematic for most systems. Typical demodulators either lock the phase from any arbitrary starting point or use differential signaling independent of phase. Likewise many other processing systems (e.g., radar) resolve initial phase as an ambiguity so arbitrary offsets are inconsequential.
Just to continue to belabor the point even further in as anal-retentive a fashion as possible, Figure 5 shows simple block diagram depictions of each method.
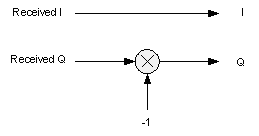
(a)
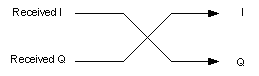
(b)
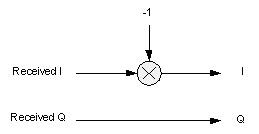
(c)
Figure 5. Signal flow depictions of the three methods of baseband spectral inversion. Invert the Q channel (a), swap the channels (b), and invert the I channel (c).
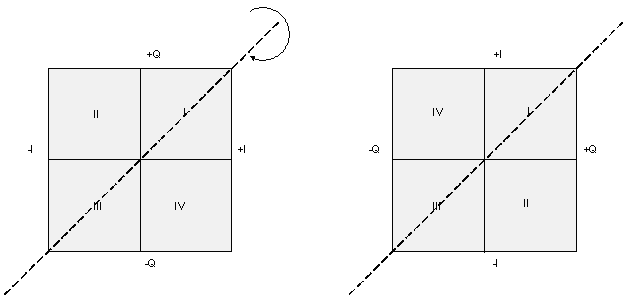
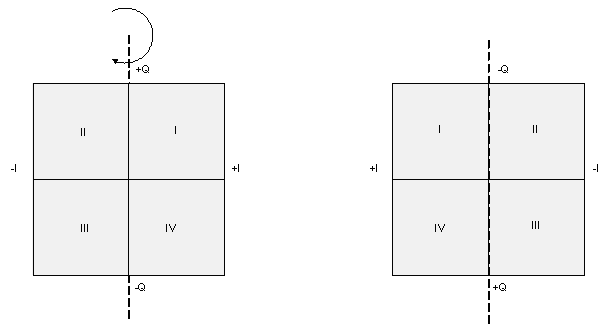
There's an interesting conceptual connection between the three methods shown and Figure 4. In Figure 4 the direction of rotation of the vector depends on which side of the I/Q plane the observer is located, as depicted by arrows A and B. If one can somehow, architecturally, change the demodulator's perspective from one side of the plane to the other, the direction would reverse and the spectrum would be inverted from what was seen on the other side. The three spectral inversion methods described can be thought of as flipping the I/Q plane one-hundred and eighty degrees (or p, if you're so inclined), about an axis. Method 1, inverting the Q channel, rotates the plane around the I axis. Method 2, swapping the I and Q channels, rotates the plane about an axis through Quadrants I and III at an angle of p/4. Method 3, inverting the I channel, rotates the plane about the Q axis. Figure 6, in the interest of maintaining maximum anal-retentiveness, depicts each method graphically.
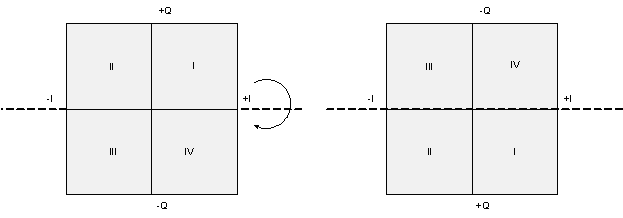
(a)
(b)
(c)
Figure 6. Graphical depiction of the three spectral inversion methods. The quadrants before and after rotation are shown, so that the reversal of rotation of a vector sweeping progressively through the quadrants becomes evident. The methods are: inversion of Q channel (a), swapping I and Q channels (b), and inversion of the I channel (c).
Summary
Correcting spectral inversion issues is trivial in baseband processing. Three very simple methods can be used, all of equal effectiveness and very low complexity. Mathematical and intuitive rationale for each method have been shown. It should be noted that the methods described are equally effective at baseband in the modulator or in the demodulator, or at any appropriate stage in a baseband (i.e., complex-valued) processing system.
Copyright © 2008, Eric Jacobsen, All Rights Reserved
References:
[1] Rick Lyons, Quadrature Signals: Complex but Not Complicated https://www.dsprelated.com/showarticle/192.php
[2] CRC, Standard Mathematical Tables and Formulae, 30th Ed., Boca Raton, CRC Press, 1996
- Comments
- Write a Comment Select to add a comment

Hi Eric,
@Rick Lyons' article: Quadrature Signals: Complex but Not Complicated can also be found on DSPRelated at:
https://www.dsprelated.com/showarticle/192.php
or in pdf format:
https://www.dsprelated.com/showabstract/3836.php
I know that Rick is really good at correcting the smallest errors in his articles and providing updates to his pdf files hosted on DSPRelated as he makes corrections. I think it would be safe to change the link in your article to the DSPRelated version but I'll let you make that call.
Thanks.

Got it. Changed it to the dsprelated link.
Congrats
Tks
Thanks, great article indeed.
I do have a comment.
This paper does not distinguish if spectral inversion is an artifact of choosing the high side or low side image when performing RF down-conversion to baseband OR is an artifact of the initial phase of a exp(-j*w*t) signal.
Up until figure 3, we are mainly concerned about the upper and lower side images from LO.
But all the trignometry math depicts fun additions to the initial phase of the downconverting signal exp(-j*w*t) signal. I am not able to tie the gap between the 2 bifurcations
Advance apologies if I have misunderstood your post.
Thanks
PS: I have read the "complex but not complicated" paper by Lyons.

Hi,
The initial phase is inconsequential, since the sign of the frequency is the determining factor. In this case the lower-case omega (which kinda shows up as "w" a lot), is angular frequency and not phase. Initial phase terms, which would usually show up as theta or phi, would typically be shown as exp(-j*(wt+phi)), but in this case we are only concerned with exp(-j(wt)) or exp(jwt) or similar. The sign of omega (w) determines whether it is positive or negative for a complex-valued signal.
I hope that helps.
Will swapping SIN/COS on the LO ports of the I and Q downconverter mixers invert the spectrum as well?

Yes, because multiplication by sin or cos essentially defines which branch is I or Q, swapping them effectively swaps the I and Q channels. So this does achieve spectral inversion by swapping the channels.
To post reply to a comment, click on the 'reply' button attached to each comment. To post a new comment (not a reply to a comment) check out the 'Write a Comment' tab at the top of the comments.
Please login (on the right) if you already have an account on this platform.
Otherwise, please use this form to register (free) an join one of the largest online community for Electrical/Embedded/DSP/FPGA/ML engineers:


















