Free Books    Introduction to Digital Filters  

Implications of Linear-Time-Invariance

Using the basic properties of linearity and time-invariance, we will derive the convolution representation which gives an algorithm for implementing the filter directly in terms of its impulse response. In other words,

$\textstyle \parbox{0.8\textwidth}{\emph{the output $y(n)$\ of any LTI filter (i... ... be computed by convolving the input signal with the filter impulse response.}}$

Figure: Input and output signals for the filter $ y(n) = x(n) + 0.9\,y(n - 1)$. (a) Input impulse $ \delta (n)$. (b) Output impulse response $ h(n)=u(n)\,0.9^n$. (c) Input delayed-impulse $ \delta (n - 5)$. (d) Output delayed-impulse response $ h(n - 5)$.
\begin{figure}\input fig/kfig2p9.pstex_t \end{figure}

The convolution formula plays the role of the difference equation when the impulse response is used in place of the difference-equation coefficients as a filter representation. In fact, we will find that, for FIR filters (nonrecursive, i.e., no feedback), the difference equation and convolution representation are essentially the same thing. For recursive filters, one can think of the convolution representation as the difference equation with all feedback terms ``expanded'' to an infinite number of feedforward terms.

An outline of the derivation of the convolution formula is as follows: Any signal $ x(n)$ may be regarded as a superposition of impulses at various amplitudes and arrival times, i.e., each sample of $ x(n)$ is regarded as an impulse with amplitude $ x(n)$ and delay $ n$. We can write this mathematically as $ x(n)\delta(\cdot - n)$. By the superposition principle for LTI filters, the filter output is simply the superposition of impulse responses $ h(\cdot)$, each having a scale factor and time-shift given by the amplitude and time-shift of the corresponding input impulse. Thus, the sample $ x(n)$ contributes the signal $ x(n)h(\cdot - n)$ to the convolution output, and the total output is the sum of such contributions, by superposition. This is the heart of LTI filtering.

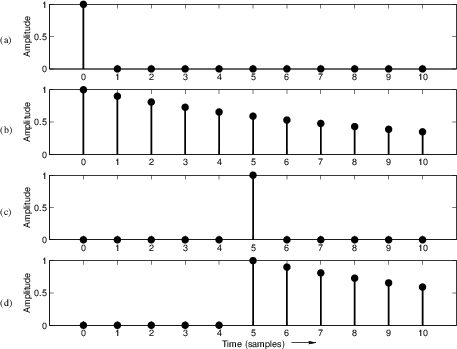
Before proceeding to the general case, let's look at a simple example with pictures. If an impulse strikes at time $ n = 5$ rather than at time $ n = 0$, this is represented by writing $ \delta (n - 5)$. A picture of this delayed impulse is given in Fig.5.2c. When $ \delta (n - 5)$ is fed to a time-invariant filter, the output will be the impulse response $ h(n)$ delayed by 5 samples, or $ h(n - 5)$. Figure 5.2d shows the response of the example filter of Eq.$ \,$(5.3) to the delayed impulse $ \delta (n - 5)$.

In the general case, for time-invariant filters we may write

$\displaystyle {\cal L}_n\{{\mbox{{\sc Shift}}_K\{\delta}\}\} \isdef {\cal L}_n\{\delta(\cdot - K)\} = {\cal L}_{n-K}\{\delta(\cdot)\} = h(n-K) $

where $ K$ is the number of samples delay. This equation states that right-shifting the input impulse by $ K$ points merely right-shifts the output (impulse response) by $ K$ points. Note that this is just a special case of the definition of time-invariance, Eq.$ \,$(4.5).

If two impulses arrive at the filter input, the first at time $ n = 0$, say, and the second at time $ n = 5$, then this input may be expressed as $ \delta(n) + \delta(n - 5)$. If, in addition, the amplitude of the first impulse is 2, while the second impulse has an amplitude of 1, then the input may be written as $ 2\delta (n) + \delta (n - 5)$. In this case, using linearity as well as time-invariance, the response of the general LTI filter to this input may be expressed as

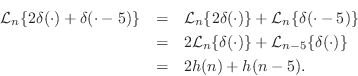
\begin{eqnarray*} {\cal L}_n\{2\delta(\cdot) + \delta(\cdot - 5)\} &=& {\cal ... ...ot)\} + {\cal L}_{n-5}\{\delta(\cdot)\} \\ &=& 2h(n) + h(n-5). \end{eqnarray*}

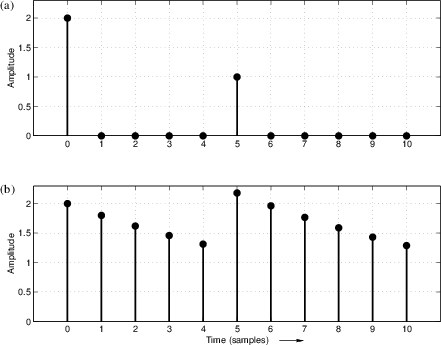
For the example filter of Eq.$ \,$(5.3), given the input $ 2\delta (n) + \delta (n - 5)$ (pictured in Fig.5.3a), the output may be computed by scaling, shifting, and adding together copies of the impulse response $ h(n)$. That is, taking the impulse response in Fig.5.2b, multiplying it by 2, and adding it to the delayed impulse response in Fig.5.2d, we obtain the output shown in Fig.5.3b. Thus, a weighted sum of impulses produces the same weighted sum of impulse responses.

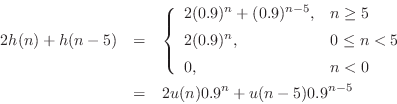
\begin{eqnarray*} 2h(n) + h(n-5) &=& \left\{\begin{array}{ll} 2(0.9)^n+(0.9)^{n... ...0 \\ \end{array} \right.\\ &=& 2u(n) 0.9^n + u(n-5) 0.9^{n-5} \end{eqnarray*}

Figure 5.3: Input impulse pair and corresponding output for the filter $ y(n) = x(n) + 0.9y(n - 1)$. (a) Input: impulse of amplitude 2 plus delayed-impulse $ 2\delta (n) + \delta (n - 5)$. (b) Output: $ 2h(n) + h(n - 5)$.
\begin{figure}\input fig/kfig2p10.pstex_t \end{figure}

Next Section:
Convolution Representation
Previous Section:
Impulse Response Example