Let  denote any continuous-time signal having a Fourier
Transform (FT)
denote any continuous-time signal having a Fourier
Transform (FT)
Let
denote the samples of

at uniform intervals of
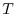
seconds,
and denote its
Discrete-Time Fourier Transform (
DTFT) by
Then the
spectrum 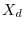
of the sampled signal
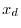
is related to the
spectrum 
of the original continuous-time signal

by
The terms in the above sum for
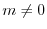
are called
aliasing
terms. They are said to
alias into the
base band
![$ [-\pi/T,\pi/T]$](http://www.dsprelated.com/josimages_new/mdft/img1790.png)
. Note that the summation of a
spectrum with
aliasing components involves addition of
complex numbers; therefore,
aliasing components can be removed only if both their
amplitude
and phase are known.
Proof:
Writing  as an inverse FT gives
as an inverse FT gives
Writing
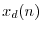
as an inverse DTFT gives
where
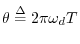
denotes the normalized discrete-time
frequency variable.
The inverse FT can be broken up into a sum of finite integrals, each of length
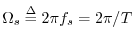 , as follows:
, as follows:
Let us now sample this representation for  at
at 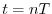 to obtain
to obtain
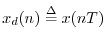 , and we have
, and we have
since  and
and  are integers.
Normalizing frequency as
are integers.
Normalizing frequency as
 yields
yields
Since this is formally the inverse DTFT of
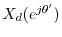
written in terms of

,
the result follows.

Next Section: Changing the BasePrevious Section: Reconstruction from Samples--The Math
![]() denote any continuous-time signal having a Fourier
Transform (FT)
denote any continuous-time signal having a Fourier
Transform (FT)
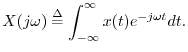

![$\displaystyle X_d(e^{j\theta}) = \frac{1}{T} \sum_{m=-\infty}^\infty X\left[j\left(\frac{\theta}{T}
+ m\frac{2\pi}{T}\right)\right].
$](http://www.dsprelated.com/josimages_new/mdft/img1788.png)
![]() as an inverse FT gives
as an inverse FT gives
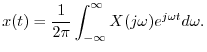
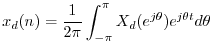
![]() , as follows:
, as follows:
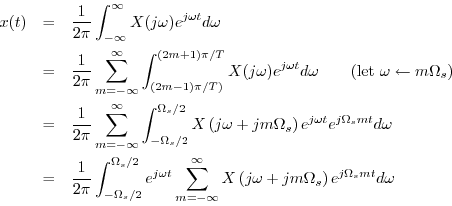
![]() at
at ![]() to obtain
to obtain
![]() , and we have
, and we have
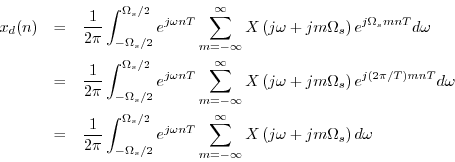
![]() and
and ![]() are integers.
Normalizing frequency as
are integers.
Normalizing frequency as
![]() yields
yields
![$\displaystyle x_d(n) = \frac{1}{2\pi}\int_{-\pi}{\pi} e^{j\theta^\prime n}
\f...
...t(\frac{\theta^\prime }{T}
+ m\frac{2\pi}{T}\right) \right] d\theta^\prime .
$](http://www.dsprelated.com/josimages_new/mdft/img1800.png)



















