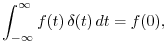Free Books
   Free Books    Mathematics of the DFT  

The Continuous-Time Impulse

An impulse in continuous time must have ``zero width'' and unit area under it. One definition is

$\displaystyle \delta(t) \isdef \lim_{\Delta \to 0} \left\{\begin{array}{ll} \fr... ...eq t\leq \Delta \\ [5pt] 0, & \hbox{otherwise}. \\ \end{array} \right. \protect$ (B.3)

An impulse can be similarly defined as the limit of any integrable pulse shape which maintains unit area and approaches zero width at time 0. As a result, the impulse under every definition has the so-called sifting property under integration,

$\displaystyle \int_{-\infty}^\infty f(t) \, \delta(t)\, dt = f(0), \protect$ (B.4)

provided $ f(t)$ is continuous at $ t=0$. This is often taken as the defining property of an impulse, allowing it to be defined in terms of non-vanishing function limits such as

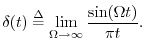
$\displaystyle \delta(t) \isdef \lim_{\Omega\to\infty}\frac{\sin(\Omega t)}{\pi t}. $

(Note, incidentally, that $ \sin(\Omega t)/\pi t$ is in $ L2$ but not $ L1$.)

An impulse is not a function in the usual sense, so it is called instead a distribution or generalized function [12,38]. (It is still commonly called a ``delta function'', however, despite the misnomer.)

Next Section:
Relation of the DFT to Fourier Series
Previous Section:
Existence of the Fourier Transform